
Esta obra está bajo licencia internacional Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0.
En la cadena de comunicación de la ciencia y la transmisión del conocimiento científico, los científicos constituyen un importante eslabón. Sin embargo, no abundan los trabajos que aborden aspectos relacionados con el papel de la comunidad científica en la divulgación de la ciencia, sus patrones de comunicación con la ciudadanía o sus pautas de comportamiento y motivaciones a la hora de participar en actividades divulgativas. Mi opinión es que los realizados hasta el momento se centran, fundamentalmente, en el estudio del papel de los distintos estamentos y en profesionales, promotores y transmisores involucrados en las tareas de divulgación científica. Con esta aportación pretendo acercar las matemáticas a un tema que la mayoría de las personas no pueden imaginarse: la enología. Mostraré solo una pincelada en la que, gracias a las diversas aplicaciones de las matemáticas, han comenzado a pensar en las matemáticas no como un tema árido solo asequible para los matemáticos, sino como una herramienta básica y fundamental que todo el mundo debería comprender tanto como pueda, porque las matemáticas pueden ayudar a esculpir y modelar casi todo, también en muchos aspectos relacionados con la bebida más importante del mundo antiguo: el vino
Palabras clave: Conocimiento, divulgación, matemáticas, epistemología, resolución de problemas, hitos científicos, enología
ABSTRACT
In the chain of communication of science and the transmission of scientific knowledge, scientists constitute an important link. However, there are not many works that address aspects related to the role of the scientific community in the dissemination of science, its patterns of communication with the public, or its patterns of behavior and motivations when participating in dissemination activities. My opinion is that those carried out so far are focused, fundamentally, on the study of the role of the different estates and on professionals, promoters and transmitters, involved in the tasks of scientific dissemination. With this contribution I intend to bring Mathematics closer to a subject that most people cannot imagine, Oenology. I will show just a brushstroke in which, thanks to the various applications of mathematics, they have begun to think of mathematics not only as a dry subject, only accessible to mathematicians, but as a basic and fundamental tool that everyone should understand, as much as you can, because mathematics can help sculpt and model almost everything, also in many aspects related to the most important drink of the ancient world, wine.
Keyword: Knowledge, divulgation, mathematics, epistemology, problem solving, scientific milestones, enology
Introducción ↑
Soy un hombre de ciencias, pero con vocación por las humanidades en sí y por la dinamización y apoyo a la docencia e investigación en mi ciudad, mi provincia, Andalucía, España e Iberoamérica, objetivos claros recogidos en los principios de la corporación que me honro en presidir, la Academia Iberoamericana de la Rábida; entre estos objetivos está la divulgación científica.
La divulgación del conocimiento, históricamente, se transforma con la llegada de nuevas técnicas y el uso de tecnologías; primero, con la aparición de la imprenta el mundo revoluciona la forma en la que se acerca a la producción científica, y en la actualidad lo digital permite un acercamiento al conocimiento que predispone una manera diferente de ver el mundo y acceder a un escenario de información que antes era inaccesible.
Así, por ejemplo, emerge el campo editorial universitario, que debe adaptarse a las nuevas dinámicas y lograr estabilizar la pérdida de legitimidad y hegemonía que vive la educación superior. Dicha situación ha impuesto un reto para lograr su permanencia en el campo de la producción científica, el cual constituye no solo la producción de conocimiento, sino también su divulgación, al articularse con las dinámicas de la contemporaneidad y la aparición de una sociedad de consumo cercana a la virtualidad.
Investigación científica ↑
El conocimiento es el acto consciente e intencional para aprehender las cualidades del objeto y primariamente es referido al sujeto, el quién conoce, pero lo es también a la cosa que es su objeto, el qué se conoce. Su desarrollo ha ido acorde con la evolución del pensamiento humano. La epistemología estudia el conocimiento y ambos son los elementos básicos de la investigación científica, la que se inicia al plantear una hipótesis para luego tratarla con modelos matemáticos de comprobación y finalizar estableciendo conclusiones valederas y reproducibles. La investigación científica (Martín y Rey, 2007) ha devenido en un proceso aceptado y validado para solucionar interrogantes o hechos nuevos encaminados a conocer los principios y leyes que sustentan al hombre y su mundo; posee sistemas propios basados en el método de hipótesis-deducción/inducción complementados con cálculos estadísticos y de probabilidades. El buen manejo de la teoría del conocimiento en investigación científica permite respuestas correctas y técnicas a cualquier hipótesis, razón por la que el investigador científico debería conocer su teoría y evolución.
Pretender acercar toda la ciencia a todo el mundo no es posible. Caben dos cuestiones para el debate: ¿debemos renunciar a todo el conocimiento científico y conformarnos con la imagen clásica de la realidad ofrecida por las humanidades? ¿Sería esto razonable? Es una pena no tener en consideración los hitos científicos más importantes, porque la ciencia nos ofrece hoy una imagen renovada, impactante y profunda de nuestra realidad humana y cosmológica (Béjar, 2017). ¿Acaso no es esto lo que siempre han buscado los humanistas? De entrada, no buscaríamos, por sí mismas, las últimas novedades científicas con el ánimo de divulgarlas y pensarlas desde la frontera del conocimiento.
No es el objetivo central de este artículo, pero sería necesario reflexionar sobre la ocupación de un amplio territorio filosófico de la teoría del conocimiento o epistemología (aunque no todo el mundo estaría dispuesto a conceder sin discusión la sinonimia de estos dos términos).
Para abordar de manera sistemática esta disciplina, deberíamos contar con una amplia gama de tópicos dedicada a afrontar el reto escéptico, para dar una caracterización general del conocimiento al problema de la verdad, de la justificación, de la percepción, la inducción, la memoria, el conocimiento a-priori, el autoconocimiento, el conocimiento de otras mentes…
En los límites difusos de este vasto espacio se sitúan las más variadas disciplinas filosóficas, algunas de ellas incluso de más reciente reconocimiento académico que la propia teoría del conocimiento. En efecto, la expresión «teoría del conocimiento» solo se forja en la primera mitad del siglo XIX y en el contexto de círculos neokantianos. Antes las reflexiones epistemológicas aparecen fundamentalmente bajo los rótulos de metafísica y lógica (Jiménez y González, 2012). A sus tradicionales y antiguas relaciones con estas estimables, venerables y respetables disciplinas se han ido sumando sus relaciones con otras mucho más recientes como especialidades reconocidas: la filosofía del lenguaje, de la ciencia, de la mente (o de la psicología), la antropología, etcétera. Como es un territorio tan vasto, no es de extrañar que por él transiten expresiones filosóficas de las más diversas procedencias. Basta una ojeada a algunos de los manuales sobre la disciplina que en los últimos años han proliferado en nuestro país para percatarse de que por ellos deambulan filósofos analíticos, fenomenólogos, teóricos críticos…, según algunos incluso hermeneutas, y habría que añadir pragmatistas de los más diversos apellidos: postestructuralistas, postmodernos, etcétera.
¿Qué es el conocimiento? ↑
Con todo ello, antes de hablar de la divulgación del conocimiento debemos plantearnos de partida qué es el conocimiento.
Según el enfoque clásico, responder a esta pregunta consiste en proporcionar las condiciones necesarias y suficientes que un individuo debe cumplir para poder decir que conoce una proposición (por ejemplo, que está nevando). El método utilizado es el de análisis conceptual (Ramírez, 2009). Los argumentos a menudo vuelven a proponer y discutir escenarios que generan intuiciones acerca de si un sujeto conoce o no la proposición en cuestión.
Este enfoque clásico a veces es criticado por estar demasiado centrado en el individuo. Descuidaría los aspectos sociales del conocimiento. Para algunos, reconocer la dimensión social del conocimiento implica reducir las nociones epistémicas, como las de justificación o verdad, a nociones puramente sociales y descriptivas. Para otros, que mantienen una concepción normativa de la epistemología centrada en la idea de la verdad, simplemente significa enriquecer el enfoque clásico (Segarra y Bou, 2004-2005) de las dimensiones sociales supuestamente irreductibles del conocimiento como creencias colectivas, procesos o instituciones productoras de conocimiento.
Es indudable que los científicos constituyen un importante eslabón en la cadena de comunicación de la ciencia y transmisión del conocimiento científico. Sin embargo, no abundan los trabajos que aborden aspectos relacionados con el papel de la comunidad científica en la divulgación de la ciencia, sus patrones de comunicación con el público o sus pautas de comportamiento y motivaciones a la hora de participar en actividades divulgativas (Iaccarino, 2011). Mi opinión es que los realizados hasta el momento se han centrado fundamentalmente en el estudio del papel de los distintos estamentos y en profesionales, promotores y transmisores, involucrados en las tareas de divulgación científica.
Matemáticas y enología ↑
Con esta aportación pretendo acercar las matemáticas a un tema que la mayoría de las personas no pueden imaginarse: la enología.
En el año 2017, preparando una conferencia de divulgación sobre la utilidad de las matemáticas en la vida real, encontré por Internet un trabajo titulado Mathematics and Wine, «Matemáticas y vino» (De Marchi, 2007). Me interesó mucho su lectura, ya que históricamente se ha ido dando —y se sigue dando en la actualidad— una situación marcada en cuanto al estudio de las matemáticas: la dificultad para aprenderlas, la incomprensión que la gente cree tener al respecto y la poca aplicabilidad que les ve en la vida social.
Consecuentemente podemos plantearnos diver sas cuestiones, entre otras: ¿ha sucedido esta situación constantemente? ¿Cuándo ha surgido la incomprensión de esta disciplina? Probablemente los profesores que han enseñado, enseñan y enseñarán han sido, son y serán responsables y copartícipes de no conseguir plenamente el logro de despertar el interés y el gusto por las matemáticas en nuestros estudiantes, de forma tal que se logre un perfecto y armónico engranaje en el binomio E/A (enseñanza/aprendizaje). También es cierto que desde la década de los setenta, fundamentalmente, en nuestro país, primero con la aparición de los movimientos de renovación pedagógica y después con la aparición de las sociedades de profesores de matemáticas, se demostró la hipótesis de que con la implantación de tareas que relacionen las matemáticas con aspectos de la vida real se disminuye el nivel de dificultad de los alumnos en la aplicación de la matemática en la resolución de problemas de nuestro entorno cotidiano (Van Loon y Sarzano, 2016). Existen infinidad de aplicaciones para mostrar y distinguir los dos tipos de matemáticas: la matemática pura, que es la que ordena y estructura el pensamiento, y la matemática aplicada como herramienta útil de manejo.
En este sentido mostraré, con brevedad por razones obvias de espacio concedido, que, gracias a las diversas aplicaciones de las matemáticas, la mayoría de las personas han comenzado a pensar en las matemáticas no solo como un tema árido únicamente asequible a los que se pueden denominar, permítame el lector la expresión, raros y chalados matemáticos, sino como una herramienta básica y fundamental que todo el mundo debería comprender tanto como pueda, porque las matemáticas pueden ayudar a esculpir y modelar casi todo, también en muchos aspectos relacionados con la bebida más importante del mundo antiguo: el vino.
Históricamente, el vino ha tenido relevancia y tradición, y ha estado presente en las más importantes manifestaciones artísticas, en escultura, poesía, teatro y novela. En los museos más prestigiosos del mundo existen cuadros que plasman escenas con las copas de vino o el decantador en un intencionado primer plano.
En el artículo citado ut supra, se muestra cómo las matemáticas también se pueden utilizar para describir muchos hechos y aspectos relacionados con el vino, especialmente con la cata, y que el vino es un sistema dinámico caótico que, gracias a las matemáticas, se puede estudiar adecuadamente. Esto puede ayudar a los enólogos y catadores a comprenderlo mejor. El vino, matemáticamente hablando, como sistema dinámico, tiene su tiempo inicial correspondiente a la elaboración del mosto, luego, tras la fermentación alcohólica, se convierte en vino y, dependiendo de sus características, podemos envejecerlo en barricas o en botellas.
Por otro lado, el investigador Shepherd (Shepherd, 2016), prestigioso neurólogo de la Universidad de Yale, ha publicado varios libros sobre neurología y neurogastronomía en los que analiza el reto para el cerebro que supone catar la complejidad casi inabarcable de los vinos, y concluye que esa labor es creativa, hasta el punto de que subtitula su libro Cómo el cerebro crea el sabor del vino (el acto de catar se ve así afectado por la edad, el sexo o la memoria). Destaco una frase suya: «Catar vinos estimula el cerebro humano tanto o más que resolver un problema de matemáticas» (sic).
Así, destaco que, aunque no lo parezca, la ciencia enológica y las matemáticas utilizan términos comunes: abierto, aristas, armónico, suave, tipificado…
La crianza de vinos se estudia con matemáticas, por ejemplo, para conocer en profundidad cómo evoluciona el vino en las tinas de madera. Con este objetivo, y valiéndose de las matemáticas como herramienta, investigadores de la Universidad de Alcalá de Henares (UAH) han iniciado en 2018 el proyecto denominado BESTAGEING. A lo largo del estudio, los investigadores profundizan en aspectos relacionados con la evolución aromática del vino durante la vinificación y el envejecimiento en tinas de madera. También ahondan en el manejo del oxígeno y las implicaciones microbiológicas que condicionan el uso de estas barricas en los distintos momentos del proceso productivo, poniendo en práctica nuevas metodologías de análisis microbiológico y sensorial.
Se deduce de lo anterior que entre el lenguaje que utiliza la enología y el que utiliza la matemática existen términos comunes. La enología como técnica y arte para producir vino es objeto de atención en el mundo universitario. Así, nuestro país —con una importante superficie vitícola y tercer país productor de vino en el mundo— aglutina a ocho universidades que, desde 1996, otorgan el título de licenciado en Enología: Universidad de la Rioja y Universidad Rovira i Virgili, Universidad de Valladolid (Campus de Palencia), Universidad Miguel Hernández, Universidad de Cádiz, Universidad de Córdoba, Universidad de Extremadura y Universidad Politécnica de Valencia. La Rioja es una referencia internacional en este sector, que precisa de profesionales formados en las más modernas técnicas de cultivo, elaboración y comercialización de este producto.
Actualmente, el grado en Enología tiene un gran componente práctico, que se desarrolla tanto en las propias instalaciones de la universidad (bodega experimental, campos de experimentación, sala de catas, laboratorios, etcétera) como en bodegas industriales.
Materias como viticultura, enología, tecnología, ingeniería, química o microbiología enológicas, matemáticas… conviven con otras vinculadas al marketing, la cultura y la legislación vitivinícola en un grado que culmina con prácticas externas en bodega industrial. Para conseguir los objetivos de estos estudios, título universitario oficial denominado grado en Enología, se debe proporcionar una formación científica adecuada en los métodos y técnicas de cultivo de viñedo con la modelización matemática en el diseño de superficies que mejoren el rendimiento en las vendimias, la construcción de la tonelería para resolver los problemas de almacenamiento, el establecimiento de ciertos criterios en la elaboración de vinos, mostos y otros derivados de la vid, análisis de los productos elaborados y almacenaje, gestión y conservación de los mismos…
Obviamente, para abordar en profundidad el tema de la importancia de la relación entre la enología y las matemáticas necesitaríamos mucho más espacio. Algunas pinceladas podrán servir para introducirnos, aunque sea a modo de curiosidad para muchos.

El Barril de Heidelberg, de 1751, tiene incluso una pista de baile encima.
Un ejemplo práctico ↑
Un barril de madera, también llamado barrica, cuba o tonel, es un recipiente de forma cilíndrica fabricado en madera que sirve como medio de almacenamiento de elementos líquidos, pero también sólidos; en el caso que nos ocupa, el vino.
A título de curiosidad, a lo largo de la historia hay constancia de la existencia de varios barriles grandes con una geometría exquisita. Desde el si glo XVI: el primero se llamaba Barril de Johann Kasimir (Cser y Wiltschko, 2007) y fue construido en 1591 por Michael Werner por encargo del soberano del Palatinado-Lautern; tenía una capacidad de 130.000 litros, pero fue destruido durante la Guerra de los Treinta Años. Además podemos citar los barriles de Karl Ludwig (1664) y Karl Philipp (1728), que también se han perdido, hasta llegar al Barril de Karl-Theodor, llamado Barril de Heidelberg (Cser y Wiltschko, 1999), que, construido en 1751, aún se conserva y tiene una pista de baile en la parte superior (Heidelberg, 1751).
La estructura del barril está formada por piezas de madera, denominadas duelas, con moldes para conseguir la forma geométrica cóncava del contorno del tonel, sujetas por aros anchos de metal, denominados abrazaderas o zunchos, cerradas con tapas planas, también de madera, llamadas asientos o fondos. Desde la Antigüedad se ha utilizado para el almacenaje y conservación de líquidos, como agua, vino, whisky, cerveza y demás procesos de destilación de múltiples granos fermentados, frutas u otros alimentos para los que el tiempo de maduración es muy dispar. Lo más frecuente es la utilización de barricas o toneles para elaborar y mejorar vinos, pero también suelen usarse para el mezclado —conocido como blended— del whisky.
Sabemos que en el siglo XVI se hicieron enormemente populares los trabajos de Arquímedes. Las técnicas del cálculo infinitesimal para el cálculo de áreas y volúmenes fueron desarrolladas ampliamente. Especialmente el astrónomo y matemático alemán Johannes Kepler, figura clave en la revolución científica, fue uno de los matemáticos que contribuyeron a estos desarrollos.
La primera mujer de Kepler murió y Kepler quedó viudo con varios hijos. En 1613 se volvió a casar, y celebró su boda en Linz (Austria). Kepler compró un barril de vino para la boda, pero no le convenció el método que usó el comerciante para medir el volumen del barril y determinar el precio. Como consecuencia de este incidente, Kepler estudió varios problemas sobre volúmenes, entre ellos cómo calcular correctamente el volumen de un barril de vino y encontrar proporciones que optimizaran ese volumen. A partir de este contratiempo, en un trabajo sistemático estudió cómo calcular áreas y volúmenes de diferentes cuerpos, especialmente cuerpos de revolución, y escribió un libro sobre este tema en 1615: Nova stereometria doliorum vinariorum («Nueva geometría sólida de los barriles de vino»).
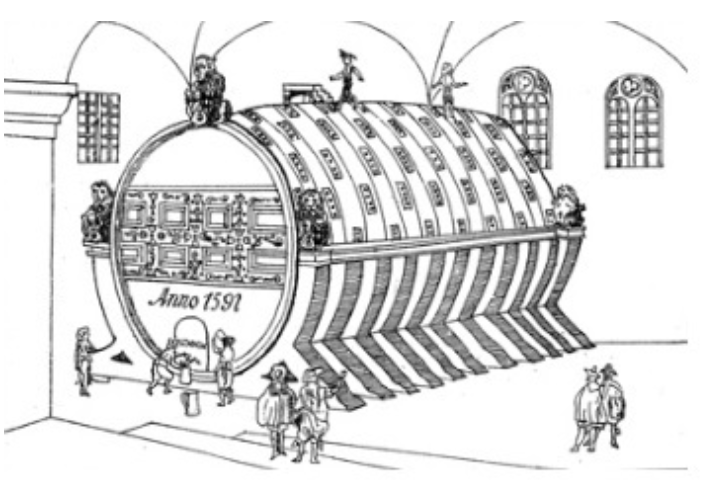
El primer barril grande se construyó en 1591.
Fuentes y bibliografía ↑
Béjar, M. (2017): Las grandes cuestiones del conocimiento científico en el siglo XXI, https://blogs.comillas.edu/FronterasCTR/2017/03/2015/cuestiones-conocimiento-cientifico-sigloxxi
BESTAGEING, Proyecto (2018), https://www.articai.es/proyecto-id-distintivo-eureka/ y https://www.tecnovino.com /el-proyecto-bestageing-aplicara-las-matematicas-para-estudiar-la-crianza-del-vino/
Cser, A., y Wiltschko, S. (1999): El gran barril en el castillo de Heidelberg. Neckargemünd-Dilsberg.
Cser, A., y Wiltschko, S. (2007): Los cuatro grandes barriles del castillo de Heidelberg. Sobre la historia de la construcción, el arte, la administración y la economía. Neckargemünd-Dilsberg.
De Marchi, S. (2007): «Mathematics and Wine», en Applied Mathematics and Computation, 192, pp. 180-190. Verona (Italia): Department of Computer Science, Universidad de Verona.
Iaccarino, A. (2011): Reflections on the Relation between Conservation and Science, https://journals.openedition.org/ceroart/2194 y https://journals.openedition.org/ceroart/2239
Jiménez, J. A., y González, D. (2012): Cambios de paradigma de la divulgación del conocimiento en la educación superior en Colombia: crisis desde el campo editorial universitario. Universidad Distrital Francisco José de Caldas.
Kasimir, B. (1591): https://www.schloss-heidelberg.de/fr/erlebnis-schloss-garten/schloss-garten/gebaeude/edifice-du-tonneau/
Kepler, J. (1615): Nova stereometria doliorum vinariorum, http://posner.library.cmu.edu/Posner/books/pages.cgi?call=520_K38PN&layout=vol0/part0/copy0
Martín, M. J., y Rey, J. (2007): El papel de los científicos en la comunicación de la ciencia y la tecnología a la sociedad: actitudes, aptitudes e implicación, https://digital.csic.es/bitstream/10261/1616/1/30_Papel.pdf
Ramírez, A. V. (2009): «La teoría del conocimiento en investigación científica: una visión actual (Knowledge’s Theory in Scientific Research: A Current Scope)», en Anales de la Facultad de Medicina, 70 (3), pp. 217-224.
Segarra, M., y Bou, J. C. (2004-2005): «Concepto, tipos y dimensiones del conocimiento: configuración del conocimiento estratégico», en Revista de Economía y Empresa, núms. 52-53, pp. 175-195.
Shepherd, G. M. (2016): Neuroenology: How the Brain Creates the Taste of Wine. Ed. Columbia University Press.
Van Loon, M., y Sarzano, M. (2016): «Quelques problèmes de la conception duale de la norme de l’action et de l’assertion», en J. M. Chevalier y B. Gaultier: La connaissance et ses raisons. La Philosophie de la Connaissance au Collège de France.