
Organizadores curriculares y finalidades de la educación: oportunidades para la mejora docente
To cite this article: Beltrán-Pellicer, P., Martínez Juste, S. y Alsina, Á. (2023). Organizadores curriculares y finalidades de la educación: oportunidades para la mejora docente. Márgenes, Revista de Educación de la Universidad de Málaga, 4(2), 7-30. https://doi.org/10.24310/mgnmar.v4i2.17177
DOI: https://doi.org/10.24310/mgnmar.v4i2.17177
 Esta obra está bajo licencia internacional Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0.
Esta obra está bajo licencia internacional Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0.
Pablo Beltrán-Pellicer 0000-0002-1275-9976
Universidad de Zaragoza (España)
pbeltran@unizar.es
Sergio Martínez-Juste 0000-0002-2607-6789
Universidad de Zaragoza (España)
sergiomj@unizar.es
Ángel Alsina 0000-0001-8506-1838
Universidad de Girona (España)
angel.alsina@udg.edu
RESUMEN:
Los currículos desarrollados en España al amparo de la LOMLOE introducen importantes novedades en su arquitectura. En este artículo, se indaga en torno a diferentes elementos cruciales de dichos currículos, con el propósito de profundizar en las relaciones de estos elementos con las finalidades de la educación y reflexionar sobre lo que deberían suponer en la práctica docente. Para ello, después de describir dichas finalidades, se abordan los principales organizadores curriculares: las competencias específicas y las situaciones de aprendizaje; el diseño de actividades y la metodología; la planificación de los procesos de enseñanza y aprendizaje; y la evaluación. Junto con un análisis de estos organizadores, se aportan ejemplos desde diversas materias, con especial énfasis en Matemáticas, para tratar de aportar algunos andamios que contribuyan a comprender las principales novedades de los currículos vigentes e incorporarlas en la práctica. Se concluye que conocer y comprender cuáles son los principales organizadores curriculares, reflexionar sobre ellos y disponer de herramientas para adaptarlos a la práctica docente, son elementos imprescindibles para mejorarla.
PALABRAS CLAVE: diseño curricular; práctica docente; evaluación; metodología
ABSTRACT:
The curricula developed in Spain under the LOMLOE regulation introduce significant changes to its architecture. This article explores various crucial elements of these curricula, aiming to delve into their relationships with the aims of education and to reflect on their implications for teaching practice. For this purpose, after describing these aims, the main curricular organisers are addressed: specific competencies and learning situations; the design of activities and the methodology; the planning of teaching and learning processes; and evaluation. Along with an analysis of these organisers, examples are provided from various subjects, with a special emphasis on Mathematics, in an attempt to offer some scaffolding that helps understand the main innovations of the current curricula and incorporate them into practice. It is concluded that understanding what the main curricular organisers are, reflecting on them and having the tools to adapt them to teaching practice are essential elements for its improvement.
KEYWORDS: curricular design; classroom practice; evaluation; teaching methods
Agradecimientos: A Violeta Delgado, por las referencias sobre el aprendizaje de Lengua extranjera.
Financiación: Investigación realizada como parte del proyecto de investigación PID2019-105601GB-I00 / AEI / 10.13039/501100011033, con apoyo del Grupo S60_23R - Investigación en Educación Matemática (Gobierno de Aragón y Fondo Social Europeo) y del proyecto de investigación 2020 ARMIF 00007 de la Agència de Gestió d’Ajuts Universitaris i de Recerca (AGAUR) de la Generalitat de Catalunya.
1. INTRODUCCIÓN
Los currículos desarrollados al amparo de la LOMLOE han vuelto a poner sobre la mesa cuestiones con cierto recorrido en nuestro sistema educativo, como “aprendizaje competencial”, que no terminan de cuajar. Tal y como señala Contreras (2022), la esencia de muchas de las ideas que tratan de reforzar los nuevos currículos ya estaba presente en el Diseño Curricular Base (1989) de la LOGSE. En otras palabras, aunque se observe fácilmente que no son los primeros currículos “competenciales” que surgen en territorio español porque LOMCE y LOE ya incluían competencias (clave o básicas), el origen de la reforma que nunca acaba de aterrizar en las aulas es más anterior todavía.
“Cuestiones que no terminan de cuajar”; “la reforma que nunca acaba de aterrizar” y otras afirmaciones similares con las que se podría seguir, evidencian cierto desasosiego, confusión y, a veces, aversión en torno a las reformas curriculares que se van sucediendo en el sistema educativo español. En su conjunto, esta situación genera muchos interrogantes: ¿qué está pasando en torno a las directrices curriculares en España?, ¿qué es lo que no se está haciendo del todo bien?, ¿qué se podría mejorar para que el currículo sea lo que realmente pretende ser? y, poniendo el foco directamente en el profesorado, ¿dónde deberíamos centrarnos para ayudar a conseguir lo que el currículo pretende? De entrada, es honesto señalar que no tenemos una respuesta amplia para todas estas preguntas, ya que requieren un abordaje multifactorial que escapa de las finalidades de este artículo. Sin embargo, empeñados por la idea que es imprescindible aportar andamios que sirvan de apoyo al profesorado para comprender mejor el nuevo escenario curricular y poder navegar por él de forma más segura y eficaz, en este artículo se intentan aclarar algunas cuestiones imprescindibles en torno a los principales organizadores curriculares.
Los nuevos currículos de todas las etapas, desde Educación Infantil hasta Bachillerato, suman en total 665 páginas (MEFP, 2022a, 2022b, 2022c, 2022d). Es evidente que, con esta extensión, hay muchas ideas que se repiten, otras que no tienen un tratamiento longitudinal claro... razón por lo que algunos autores, como por ejemplo de Azcárraga (2022), hacen alusión al exceso normativo o la absurdidad de algunas entradas. Otros autores, como Alsina y Rodríguez-Muñiz (2021), se refieren a la necesidad de buscar medios alternativos para la mejora docente, quizás menos formales, pero que proporcionen la información de forma más sintetizada para poder acceder a ella sin tanta inversión de tiempo. En este sentido, se considera que un ejercicio interesante a realizar desde la Administración es tratar de proporcionar guías rápidas, más que extender y repetir las directrices curriculares en documentos interminables.
Dicho esto, los nuevos currículos incorporan importantes novedades como el perfil de salida, las competencias específicas y su relación con los criterios de evaluación y elementos como las situaciones de aprendizaje. Aquí se asume que es altamente recomendable que el profesorado conozca y comprenda bien estas novedades y tenga herramientas para incorporarlas en la práctica docente. Para ello, el artículo aborda, en primer lugar, las finalidades de la educación, con el propósito de ofrecer un horizonte sencillo, pero no por ello menos riguroso, de los fundamentos en los que se debería sustentar la práctica docente. Seguidamente, se indaga en torno a los principales organizadores curriculares, que se ejemplifican desde las distintas materias, con mayor peso de la Matemática al ser la disciplina de referencia de los autores: 1) las competencias específicas y las situaciones de aprendizaje, tanto para dejar claro el engranaje del currículo como para desmitificar la forma de materializar el aprendizaje del alumnado, que ha generado mucho ruido; 2) el diseño de actividades y la metodología, haciendo especial hincapié en el aprendizaje a través de la resolución de problemas, las actividades ricas y la inclusión; 3) la planificación de los procesos de enseñanza y aprendizaje, rompiendo algunos mitos acerca de la programación; y, 4) la evaluación y la calificación, rompiendo algunos de sus principales mitos. A lo largo de este artículo, como se ha señalado, se intenta desgranar la relación de estos organizadores con las finalidades de la educación, así como reflexionar sobre lo que deberían suponer en la práctica docente.
2. FINALIDADES DE LA EDUCACIÓN
—Profe, ¿por qué tengo que aprender matemáticas?
Un currículo de Matemáticas —y esto sería extensible, obviamente, al resto de materias— trata de dar respuesta a esta pregunta. En realidad, se trata de, por un lado, discernir cuáles son las finalidades de la educación y, por otro lado, articular un documento que describa qué debería pasar en las aulas para cumplir con esas finalidades.
Se puede responder de varias maneras. Si decimos que las Matemáticas son necesarias para el día a día, porque requerimos de ellas para saber a qué precio nos sale un producto tras aplicar el descuento o para decidir si una mesa cabrá por el vano de la puerta sin tener que moverla, estamos aludiendo a una finalidad aplicada, de tipo social. Es decir, no puedes desenvolverte en sociedad si no aprendes matemáticas. Hay otra finalidad, pero de carácter instrumental, a la que nos referimos cuando decimos que sin aprender matemáticas no puedes acceder a determinados estudios o trabajos.
No obstante, hay otras finalidades. Así, es habitual escuchar aquello de “necesitas aprender matemáticas porque te amuebla la cabeza”. Igualmente, podemos responder que una de las razones de ser de las matemáticas escolares es que permite desarrollar la creatividad, la resolución de problemas, etc. En estos casos estamos aludiendo a una finalidad formativa, porque nos hace crecer como personas.
También se podría responder a la incómoda pregunta sin ningún fundamento, con un tajante “porque sí” o con un “porque es estupendo aprender matemáticas”. En cualquier caso, todas estas finalidades se explicaban muy bien ya en el marco de la LOGSE, cuando en el Anexo 1 del Real Decreto 1006/1991, de 14 de junio, por el que se establecen las enseñanzas mínimas correspondientes a la Educación Primaria, se subrayaron tres aspectos —formativo, funcional e instrumental— a los que debería responder la enseñanza de las matemáticas:
Así pues, a lo largo de la educación obligatoria las matemáticas han de desempeñar, indisociable y equilibradamente, un papel formativo básico de capacidades intelectuales, un papel aplicado, funcional, a problemas y situaciones de la vida diaria, y un papel instrumental, en cuanto armazón formalizador de conocimientos en otras materias. Todo ello justifica, en una línea no siempre coincidente con la tradicional, los contenidos de las matemáticas en esta etapa, así como las características didácticas básicas de su enseñanza. (p. 31)
Posteriormente, además de ir reproduciéndose en los decretos derivados de otras leyes posteriores de educación, esta idea la han recogido también diversos autores como Godino (2004) y Alsina (2011):
La enseñanza y el aprendizaje de las matemáticas ha de atender equilibradamente a: a) al establecimiento de destrezas cognitivas de carácter general, susceptibles de ser utilizadas en una amplia gama de casos particulares, que potencian las capacidades cognitivas de los alumnos; b) a su aplicación funcional, posibilitando que los alumnos valoren y apliquen sus conocimientos matemáticos fuera del ámbito escolar, en situaciones de la vida cotidiana; c) a su valor instrumental, creciente a medida que el alumno progresa hacia tramos superiores de la educación, y en la medida en que las matemáticas proporcionan formalización al conocimiento humano riguroso y, en particular, al conocimiento científico. (Godino, 2004, p. 95)
El uso de contextos en la clase de matemáticas, pues, puede contribuir a facilitar el aprendizaje de esta disciplina, pero sobre todo a comprender cuál es el sentido de las matemáticas, cuáles son sus verdaderas funciones: formativa, teniendo en cuenta que los contextos permiten pasar progresivamente de situaciones concretas o situaciones abstractas (matematización progresiva); instrumental, al considerar que los contextos son, en realidad, herramientas que favorecen la motivación, el interés o el significado de las matemáticas; y aplicada, al fomentar el uso de las matemáticas en contextos no exclusivamente escolares y, por lo tanto, contribuir a la formación de personas matemáticamente más competentes. (Alsina, 2011, p. 14)
Como ya se ha señalado, estas finalidades son extensibles —de un modo u otro— al resto de materias del currículo. Comprenderlas, asumirlas y adaptarlas a cada materia es muy útil para dar sentido a la labor docente y tener una hoja de ruta clara sobre qué hacer y, sobre todo, porqué hacerlo. Desde esta perspectiva, a continuación, se abordan los principales organizadores curriculares de los nuevos currículos de la LOMLOE y se establecen relaciones con las finalidades de la educación descritas.
3. ORGANIZADORES CURRICULARES
Como se ha señalado, en esta sección se abordan los principales organizadores curriculares, que pueden ser oportunidades para mejorar la práctica docente: las competencias específicas y las situaciones de aprendizaje; el diseño de actividades y la metodología; la planificación de los procesos de enseñanza y aprendizaje; y la evaluación y la calificación.
3.1. Competencias específicas y situaciones de aprendizaje
La idea de plantear los aprendizajes en términos de competencias ha sido impulsada mayoritariamente por la OECD, pero no es algo exclusivo de esta organización (Fernández-Navas, 2015, pp. 187-188). Organismos como la International Association for K-12 Online Learning (iNACOL), por ejemplo, llevan mucho tiempo trabajando también en sistemas de educación basados en competencias (Casey y Sturgey, 2018).
En la legislación educativa española, que es el marco legal que se analiza en este artículo, el enfoque competencial se incorpora por primera vez en la LOGSE a partir de la definición de competencias básicas, que se referían a aprendizajes imprescindibles para la realización personal del alumnado, el ejercicio de la ciudadanía activa, la incorporación a la vida adulta de manera satisfactoria y el desarrollo de un aprendizaje permanente a lo largo de la vida. Más adelante, considerando la Recomendación del Parlamento Europeo y del Consejo, de 18 de diciembre de 2006, sobre las competencias clave para el aprendizaje permanente, las competencias básicas se substituyen por competencias clave, que se refieren a capacidades para aplicar de forma integrada los contenidos propios de cada enseñanza y etapa educativa, con el fin de lograr la realización adecuada de actividades y la resolución eficaz de problemas complejos.
En la LOMLOE, la caracterización de las competencias clave se actualiza a partir de la Recomendación del Consejo de la Unión Europea, de 22 de mayo de 2018 relativa a las competencias clave para el aprendizaje permanente: se trata de desempeños imprescindibles para que el alumnado pueda progresar con garantías de éxito en su itinerario formativo y afrontar los principales retos y desafíos globales y locales. Así, pues, como señalan Beltrán-Pellicer y Alsina (2022), la idea de competencia se va modificando con el tiempo: primero, se vincula a aprendizajes; seguidamente a capacidades; y, actualmente, a desempeños, lo cual pone de manifiesto que se trata de un concepto dinámico, en constante evolución y difícil de definir.
En la nueva ley, además, se introduce como novedad la definición de competencias específicas, que son objeto de análisis en el siguiente subapartado.
3.1.1. Las competencias específicas
En los decretos derivados de la LOMLOE (MEFP, 2022a, 2022b, 2002c, 2022d) es la primera vez que se definen competencias específicas en cada materia. De acuerdo con Beltrán-Pellicer y Alsina (2022) la concreción de estas competencias aporta funcionalidad, ya que la generalidad de las competencias clave no resultaba práctica. Desde este marco, para desarrollar esta sección, se realiza un análisis de contenido de la legislación educativa y se hace hincapié en su aterrizaje en las aulas.
Lo primero que llama la atención es que el término “competencias específicas” no aparece ninguna vez en la LOMLOE, y no es hasta el despliegue de la ley en los decretos en los que se establece la ordenación y las enseñanzas mínimas de las diferentes etapas cuando, para cada una de las materias, se fijan las competencias específicas previstas para la etapa, así como los criterios de evaluación y los contenidos enunciados en forma de saberes básicos (MEFP, 2022a, 2022b, 2022c, 2022d). Aunque en tales documentos no se argumenta a qué responde la concreción de estas competencias, más allá de lo que se acaba de exponer, sí que se aporta una definición:
Competencias específicas: desempeños que el alumnado debe poder desplegar en actividades o en situaciones cuyo abordaje requiere de los saberes básicos de cada área. Las competencias específicas constituyen un elemento de conexión entre, por una parte, las competencias clave y, por otra, los saberes básicos de las áreas y los criterios de evaluación. (MEFP, 2022a, p. 4; 2022d, p. 6)
Competencias específicas: desempeños que el alumnado debe poder desplegar en actividades o en situaciones cuyo abordaje requiere de los saberes básicos de cada área o ámbito. Las competencias específicas constituyen un elemento de conexión entre, por una parte, el Perfil de salida del alumnado, y, por otra, los saberes básicos de las áreas o ámbitos y los criterios de evaluación. (MEPF, 2022b, p. 6; 2022c, p. 7)
Una primera cuestión que podría ser objeto de cierta confusión es que la definición no es idéntica en las cuatro etapas: mientras que en las etapas obligatorias (primaria y secundaria) las competencias específicas se conceptualizan como un puente entre el Perfil de salida del alumnado y los saberes y criterios de evaluación de cada área, en las etapas no obligatorias (infantil y bachillerato), la conexión es entre las competencias clave y los saberes y criterios de evaluación de cada área o ámbito.
Otra cuestión que merece ser resaltada es que, en el decreto de infantil, el término “competencias específicas” aparece 19 veces en un documento de 33 páginas; en primaria, 51 veces en un documento de 109 páginas; en secundaria, 109 veces en un documento de 198 páginas; y, en bachillerato, 206 veces en un documento de 325 páginas. Es en este sentido que de Azcárraga (2022) apela a un exceso normativo, no tanto por el número de veces que aparece el término en cada documento, sino por su excesiva extensión:
El número exacto de veces carece de interés, pero, ignorando por el momento el contenido, asombra el orden de magnitud (...), la cifra debería bastar para cuestionar semejante pulsión legislativa ante cualquiera con sentido de la proporción; menos de la mitad de las páginas bastaría. Y no solo es relevante lo que incluyen los muy repetitivos textos, sino lo que no recogen. (p. 112)
Es evidente que este factor puede ser ya un primer obstáculo para que docentes inmersos en un sinfín de tareas burocráticas, además de las propiamente docentes, accedan a los documentos y profundicen en ellos como sería deseable. ¿Quizás sería oportuno, por ejemplo, ofrecer guías rápidas previas al despliegue de toda la normativa?
Al margen de estas cuestiones, una primera idea común que arrojan las definiciones de los tres documentos es que las competencias específicas son el marco para desarrollar las competencias clave, ofreciendo una concreción mucho mayor de qué es lo que se espera del alumnado para cada una de las materias al finalizar cada etapa. En este sentido, de una forma u otra, es altamente recomendable tener un amplio control y dominio de estas competencias específicas para que la práctica docente contribuya de manera eficaz a su desarrollo. Con ello, se quiere decir que el profesorado, primero, debería conocer cuáles son las competencias específicas de cada área (en el caso de infantil) o ámbito (para el caso de primaria, secundaria y bachillerato); segundo, debería tener herramientas de apoyo para identificar posibles lagunas de conocimiento en relación a cada competencia específica, a través por ejemplo de la observación y la reflexión sistemática de la propia práctica; y, tercero, debería establecer y priorizar estrategias tanto individuales como colectivas (por ejemplo, con todo el claustro de profesores), para formarse en relación a estas lagunas. Sin estas tres acciones, la mejora en la educación no es posible.
En el caso de las matemáticas, por ejemplo, se establecen competencias específicas estrechamente vinculadas con los estándares de procesos matemáticos del NCTM (2000): resolución de problemas, razonamiento y prueba, comunicación, conexiones y representación, además del pensamiento computacional y el sentido socioafectivo. Lamentablemente, es el propio currículo el que, o bien por omisiones o por falta de claridad en algunas entradas, no acaba de ayudar para llevar a cabo estas tres acciones: en el currículo de infantil, no se explicitan suficientemente las formas de adquisición y uso de los contenidos matemáticos a través de los procesos mencionados (Alsina, 2022a); en el currículo de primaria, aunque hay algunas entradas que se prestan a confusión, la definición de las competencias específicas puede resultar interesante para todo aquel que esté interesado en una visión de la enseñanza basada en pensar y hacer a través de los procesos (Beltrán-Pellicer y Alsina, 2022); y en los de secundaria y bachillerato, la tendencia es similar.
Una segunda idea común es que el abordaje de las competencias específicas requiere de los saberes básicos de cada área. Aquí emerge un primer dilema, que hace referencia a la concreción de dichos saberes. En el caso español, se ha optado por: a) definir saberes básicos, para evitar largas listas de contenidos; b) organizar los saberes en ciclos que corresponden a franjas de edad, tanto en la enseñanza obligatoria (6-8, 8-10, 10-12, 12-15 y 15-16 para primaria y secundaria) como no obligatoria (0-3, 3-6 y 16-18 para infantil y bachillerato). Como en el caso de las competencias específicas, es necesario que el profesorado de las diferentes etapas tenga identificados los saberes del currículo de cada área o ámbito (en el nivel que se desempeña y en los anteriores y posteriores), identifique posibles lagunas de conocimiento y establezca estrategias para mejorarlas. Adicionalmente, deben tomarse decisiones sobre cómo se abordan las competencias específicas a través de los saberes. Y es aquí donde emerge un segundo dilema, de gran envergadura, que se trata a continuación para el caso concreto de las matemáticas.
Los saberes matemáticos, por ejemplo, se estructuran en torno a sentidos que consideran las dimensiones cognitiva y afectiva: sentido algebraico, de la medida, espacial, estocástico, numérico y socioafectivo. Como ya se ha precisado anteriormente, la concreción de los saberes tiende a no ser extensiva, y se fundamenta principalmente en las ideas clave o grandes ideas matemáticas (Charles, 2005; Toh y Yeo, 2019). El CEMat (2021) ha concretado de una forma en general muy coherente estas ideas desde infantil hasta bachillerato (0-18 años), aunque en no todos los casos se ha reflejado en los currículos correspondientes: en infantil, tanto la organización por áreas globalizadas de aprendizaje como las lagunas identificadas en la concreción de los saberes matemáticos, en contraste con lo que señala la investigación en educación matemática infantil (Alsina, 2022b), puede entorpecer seriamente la labor del profesorado de esta etapa para identificar los saberes a abordar; en primaria, secundaria y bachillerato, además de repetirse la misma tendencia que en el caso de las competencias específicas (Beltrán-Pellicer y Alsina, 2021), se echa en falta una de las principales finalidades de la descripción de los saberes a partir de las ideas clave o grandes ideas: conseguir que el alumnado vea las matemáticas como un sistema altamente conectado de pensamiento y conceptos a través de varios temas, en lugar de verlos como conceptos aislados (Alsina y Bosch, 2022). Este aspecto ha sido recogido, por ejemplo, en el currículo de matemáticas de Singapur, donde se destaca que es necesario “desarrollar una mayor conciencia de la naturaleza de las matemáticas y las grandes ideas que son centrales de la disciplina” (Singapore Ministry of Education, 2018, p. 9) con el fin de lograr la coherencia entre los diferentes temas.
Por lo que respecta a cómo abordar las competencias específicas a través de los saberes, Alsina (2021) señala que es altamente estratégico tomar decisiones sobre qué saberes se seleccionan para abordar cada una de las competencias matemáticas específicas, considerando que el conjunto de saberes que se abordan durante un curso escolar debe haber cubierto las distintas competencias específicas al finalizar dicho curso. Esta es una decisión fundamental de centro porque aporta objetividad y concreción a la acción docente, puesto que tratar de afrontar todas las competencias específicas a través de todos los saberes es inasumible y muy poco operativo en la práctica.
Finalmente, una tercera idea común que emerge de la definición de competencia específica es que su nivel de desempeño se analiza a través de los criterios de evaluación. Aunque esta cuestión se desarrolla de forma más profunda en otra sección de este mismo artículo, vale la pena detenerse un momento en su conceptualización y estructuración en los documentos normativos. Por un lado, en los currículos de todas las etapas, los criterios de evaluación se consideran “referentes que indican los niveles de desempeño esperados en el alumnado en las situaciones o actividades a las que se refieren las competencias específicas de cada (área, materia o ámbito) en un momento determinado de su proceso de aprendizaje” (MEFP, 2022a, p. 5; 2022b, p. 6; 2022c, p. 7; 2022d, p. 6); por otro lado, a pesar de que se trata de criterios competenciales, aparecen desglosados por ciclos. De la conceptualización, aunque no se indica explícitamente, se desprende que los criterios de evaluación ponen el foco en las formas de adquisición y uso de los saberes; de la estructuración por ciclos, que los mismos criterios se mantienen a lo largo de la escolaridad. Estos planteamientos tienen importantes repercusiones tanto para la práctica docente como para la evaluación de la enseñanza: la planificación, la gestión y la evaluación de las actividades o situaciones de aprendizaje de los saberes de cada área o ámbito se debería pensar y llevar a cabo desde unos mismos criterios de evaluación (para cada área o ámbito), que se refieren a desempeños (destrezas o habilidades) que se van desarrollando progresivamente a lo largo de la escolaridad. Esto es lo que, a nuestro entender, daría coherencia y sentido.
En el caso de las matemáticas, apoyando las tesis de Azcárraga (2022), Beltrán-Pellicer y Alsina (2022) indican que el hecho de que los criterios de evaluación se especifiquen por ciclos:
conduce a que prácticamente cambien algunas palabras entre ciclo y ciclo, y a ciertas incoherencias, añadiduras u omisiones sin mayor razón de ser. No obstante, esto puede ser debido a que se ha querido mantener el mismo marco de diseño curricular para todas las materias, habiendo otras en las que, quizá, encaje más la diferenciación de criterios competenciales por ciclos.
Pero, más allá de esta cuestión, lo que nos parece relevante es que los criterios de evaluación, que se estructuran en torno a los ejes de resolución de problemas, el razonamiento y la prueba, la comunicación y la representación, las conexiones y destrezas socioafectivas, son el marco a partir del cual se deberían planificar, gestionar y, lógicamente evaluar, las actividades o situaciones de aprendizaje.
3.1.2. Las situaciones de aprendizaje
Resulta inquietante la confusión que se ha generado alrededor de las situaciones de aprendizaje. Sobre todo, teniendo en cuenta que la definición prescriptiva es muy clara: “situaciones y actividades que implican el despliegue por parte del alumnado de actuaciones asociadas a competencias clave y competencias específicas y que contribuyen a la adquisición y desarrollo de las mismas” (MEFP, 2022a, p. 5; 2022b, p. 6; 2022c, p. 7; 2022d, p. 6).
Para infantil, y considerando que el currículo se organiza en tres áreas globalizadas de aprendizaje, se indica que:
Las situaciones de aprendizaje deben plantear un reto o problema de cierta complejidad en función de la edad y el desarrollo del niño a la niña, cuya resolución creativa implique la movilización de manera integrada de lo aprendido en las tres áreas en las que se organiza la etapa, a partir de la realización de distintas tareas o actividades. (MEFP, 2022a, p. 33)
Para las etapas de Primaria, Secundaria Obligatoria y Bachillerato, en las que los respectivos currículos se organizan en ámbitos o materias, las situaciones de aprendizaje se materializan como:
Propuestas pedagógicas que, partiendo de los centros de interés de los alumnos y las alumnas, les permitan construir el conocimiento con autonomía y creatividad desde sus propios aprendizajes y experiencias. Las situaciones de aprendizaje representan una herramienta eficaz para integrar los elementos curriculares de las distintas áreas y actividades significativas y relevantes para resolver problemas de manera creativa y cooperativa, reforzando la autoestima, la autonomía, la reflexión y la responsabilidad. (MEFP, 2022b, p. 108; MEFP, 2022c, p. 179; MEFP, 2022d, p. 324)
Este es el marco normativo, no hay más. A partir de aquí, ha surgido un gran debate sobre a lo que se le puede llamar de situación de aprendizaje, que se asocia a diversos mitos que es necesario desmontar. Aquí se va a tratar el más difundido hasta el momento: en el argot de los docentes, ha ido floreciendo la idea que las situaciones de aprendizaje deben partir de un contexto y que dicho contexto, se refiere una situación real o de vida cotidiana.
Para desmontar este mito, vamos a referirnos a un ejemplo desde las matemáticas. Lo que conocemos como figuras geométricas son abstracciones a partir de formas y cuerpos del mundo real. Por eso, en un primer nivel de razonamiento, como el que tienen los niños pequeños, podemos llegar a decir que un rectángulo es como una puerta, que un cuadrado es como una ventana o que determinada forma es puntiaguda. Cuando el alumnado progresa en los niveles de razonamiento y, como docentes, pretendemos trabajar clasificaciones de cuadriláteros, lo haremos con entidades abstractas, no con puertas o ventanas. De hecho, ya en Educación Infantil se trabaja con estas entidades abstractas de forma manipulativa, con material como los bloques lógicos de Dienes.
¿Una actividad de clasificación de cuadriláteros con criterios exclusivos, primero, e inclusivos, después, no es una situación de aprendizaje? Dependerá de cómo se plantee y el espacio que dé a la movilización de competencias específicas, pero el hecho de que el contexto sea intra-matemático es irrelevante. Además, el término “contexto” en matemáticas no implica algo real necesariamente. Y, “cercano” no implica relación con la vida cotidiana, sino que sea significativo. Evidentemente, existirá un problema cuando introducimos capas de abstracción innecesarias.
En esta línea de pensamiento nos encontramos con esta cita de Van Den Heuvel-Panhuizen (2005), autora representativa de la escuela holandesa conocida como “Enseñanza Matemática Realista” (Realistic Mathematics Education), a la que no se le puede acusar de ignorar el papel del contexto en el aprendizaje:
El mundo de la fantasía o de los cuentos de hadas e incluso el mundo formal de las matemáticas [como los cuadriláteros de nuestro ejemplo] pueden proporcionar contextos adecuados para un problema, siempre que sean reales en las mentes de los alumnos y puedan experimentarlos como tales.
Desde el ámbito de la educación matemática, pues, “un contexto es una situación más o menos problemática que puede ser objeto de estudio y que genera preguntas o problemas que requieren las matemáticas para contestarlas o resolverlas” (Alsina, 2011, p. 13). Desde esta perspectiva, en matemáticas un contexto no debería entenderse sólo como el contexto del aula; el contexto social o familiar de la escuela o del alumno; o el contexto histórico, sino que es un término mucho más general que engloba todas aquellas situaciones y actividades que tienen sentido para el alumno y fomentan su pensamiento matemático crítico (Niss, 1995).
3.2. Diseño de actividades y Metodología
A pesar de lo que pueda leerse en redes sociales o comentarse en los claustros de los centros educativos, los nuevos currículos no prohíben explícitamente ninguna metodología. No obstante, la clave de todo está en el desarrollo y movilización de las competencias clave y específicas. Tanto que, como ya se ha señalado, los criterios de evaluación se relacionan exclusivamente con estas competencias. En ese sentido, es cierto que hay metodologías más coherentes que otras con el desarrollo de esas competencias. Imaginemos un esquema de clase de Matemáticas similar a este:
- Corregir los ejercicios mandados como tarea para casa el día anterior (tanto si es el profesor como si es un alumno el que sale a la pizarra).
- Durante gran parte del tiempo restante, exponer la “teoría” sobre cómo se hace cierto tipo de ejercicio, quizá, mediante un ejemplo resuelto.
- Dejar un tiempo en clase para que los alumnos practiquen con ejercicios similares.
Nos podemos preguntar qué competencias específicas se movilizan ahí y en qué momento.
En los Reales Decretos de Enseñanzas Mínimas de las distintas etapas, a partir de Educación Primaria (MEFP, 2022b, 2022c, 2022d) se menciona de manera explícita el papel que debe jugar la resolución de problemas y que, en el fondo, va más allá de una metodología de enseñanza. La resolución de problemas se presenta como el eje vertebrador de los contenidos (saberes). Es decir, no se trata de una serie de procesos que tienen lugar al final del tema, después de haber “visto” los saberes correspondientes, sino que estos se construyen a partir de la resolución de problemas. Aquí resulta muy clara la inspiración en los Principios y Estándares del NCTM (2000, p. 52): “Los programas de enseñanza de todas las etapas deben permitir a todos los alumnos adquirir nuevos conocimientos matemáticos mediante la resolución de problemas”.
Autores como Cai y Lester (2010) revisitan estas ideas, subrayando la importancia que tiene la enseñanza a través de la resolución de problemas para el aprendizaje del alumnado. Estos autores argumentan que la resolución de problemas no debería enseñarse como un tema independiente en el currículo de matemáticas. Al contrario, sugieren que enseñar a los estudiantes a usar estrategias generales de resolución de problemas tiene poco impacto en su éxito como solucionadores de problemas. Esta afirmación implica que no debemos detener las clases regulares para resolver problemas “tipo olimpíada” que permitan trabajar las heurísticas de resolución de problemas, como propuso Polya (1945). Más bien, la resolución de problemas debería ser un elemento transversal que condicione todo el currículo. Esto no descarta que podamos dedicar algunas sesiones a este tipo de problemas, pero el objetivo principal debe ser tratar los problemas en un sentido amplio, como tareas que permitan que el contenido matemático surja de manera natural.
En palabras de Cai y Lester (2010), la resolución de problemas debe interpretarse como una parte integral del aprendizaje de las matemáticas, y requiere un compromiso significativo en el currículo en cada nivel y en cada tema matemático. Los docentes deben ser estratégicos en la selección de tareas adecuadas y en la organización del discurso en el aula para maximizar las oportunidades de aprendizaje. Este enfoque pone más énfasis en la selección o diseño de tareas ricas en lugar de en actividades que maquillen la actividad matemática. El objetivo no es simplemente “enganchar” al estudiante, sino proporcionar tareas significativas y ricas en contenido que respondan al enfoque competencial: pensar y hacer (Alsina et al., 2021). Esto puede ser un desafío, pero es factible y los estudiantes suelen responder positivamente.
Los profesores deben involucrar a los estudiantes en una variedad de actividades de resolución de problemas, tales como encontrar múltiples estrategias de solución para un problema, participar en la exploración matemática, justificar sus soluciones y hacer generalizaciones. Centrar la enseñanza en la resolución de problemas no solo mejora el desarrollo de las habilidades de pensamiento de orden superior de los estudiantes, sino que también refuerza sus actitudes positivas hacia las matemáticas.
Esta visión de la actividad matemática basada en pensar y hacer acarrea, muchas veces, una confrontación con nuestras creencias como docentes acerca de lo que es la educación matemática. De esta manera, surgen dudas e inquietudes. Una muy habitual es que se pierde mucho tiempo con una enseñanza a través de la resolución de problemas, a pesar de que los procesos que marque el currículo exijan ese tipo de trabajo en el aula. Construir conocimiento implica dar la oportunidad de darle sentido. Dado que un currículo es mucho más que un “temario” (una colección de contenidos), el hecho de que un saber como el teorema de Pitágoras haga su aparición en la pizarra como a2+b2=c2 y se haga una página de ejercicios de aplicación de dicha fórmula no significa que se pueda “dar por dado”. Los docentes, por emplear la jerga curricular, habremos cumplido con nuestro cometido si en el proceso de abordar este saber se han movilizado competencias específicas.
Cuando enseñar a través de la resolución de problemas supone un cambio para el alumnado se produce una ruptura del contrato didáctico. La resistencia que muestra el alumnado ante un cambio en la cultura de aula ha sido ampliamente estudiada (Brown y Coles, 2013; Sullivan et al., 2015), sugiriendo que para superar esa ruptura es necesaria una coherencia constante e incansable, que lleva su tiempo, entre la práctica de aula y la cultura de aula que se pretende formar. Es decir, si el objetivo es que la resolución de problemas vertebre la actividad matemática, no podemos reducirla a una visita anecdótica al final de cada tema, después de —supuestamente— haber trabajado los contenidos. Tampoco ayuda que las pruebas de evaluación atiendan mayoritariamente a tareas mecanicistas o memorísticas. Cuando el alumnado percibe que el docente no da valor a los problemas (por el motivo que sea), actúa en consecuencia.
Una preocupación común es que centrarse en la resolución de problemas podría llevar a los estudiantes a descuidar sus habilidades básicas. Sin embargo, Cai y Lester (2010) argumentan que no hay evidencia que respalde esta preocupación. Más bien, sugieren que la pregunta debería ser: ¿qué queremos que aprendan nuestros alumnos? ¿Es más importante que puedan realizar operaciones con fracciones rápidamente, o que sean capaces de plantear y resolver problemas de manera efectiva? En un enfoque de enseñanza a través de la resolución de problemas, los contenidos se trabajan con sentido y se presta atención a la diversidad en ambos extremos del espectro de habilidades.
Esto último es importante, puesto que la normativa es muy clara al apostar por un enfoque inclusivo. Esto quiere decir que la práctica docente, en este aspecto, no debe limitarse a dar unas fichas diferentes para los que van “rezagados” y material adicional para los que tienen mayor capacidad. En ese sentido, estaríamos hablando de enseñanza diferenciada, no de inclusión. La inclusión efectiva se produce cuando la tarea de clase es la misma para todos, ofreciendo múltiples oportunidades para aprender y para, en definitiva, construir conocimiento.
La nueva normativa, al tratar la inclusión, los principios del Diseño Universal para el Aprendizaje; “es decir, la necesidad de proporcionar al alumnado múltiples medios de representación, de acción y expresión y de formas de implicación en la información que se le presenta.” (LOMLOE, 2020, p. 6). Merece la pena observar que aquí existen dos capas diferentes al diseñar tareas de aula. Por un lado, que sean accesibles para todos. Por ejemplo, si tenemos un alumno con dislexia que se va a beneficiar de emplear un tipo de fuente concreto, basta con elaborar todos los textos con ese tipo de fuente, sin necesidad de diferenciar. Por otro, con las especificidades propias de cada materia, hay que facilitar múltiples oportunidades de aprendizaje.
En matemáticas esto tiene su mejor expresión, quizás, en la definición de actividades de suelo bajo y techo alto (LTHC, por sus siglas en inglés), expresión muy empleada por NRICH (https://nrich.maths.org/10345) e inspirada en el principio del diseño del lenguaje de programación LOGO de Seymour Papert (1980). Estas actividades se basan en que todo el alumnado puede, o mejor (debe) empezar. De esta forma, el suelo bajo es un umbral que debe ser matemáticamente accesible para todos y que, obviamente, variará con la propuesta y los alumnos a la que va dirigida. Es decir, todos deben tener conocimientos matemáticos previos necesarios para comenzar a trabajar en el problema. Además, todos pueden (deben) tener la oportunidad de atascarse en algún momento, pues de lo contrario… ¿estaríamos ante un problema o ante un ejercicio? Conviene observar que el techo alto no considera solo el contenido matemático al que se puede llegar, pues es posible que algunos problemas requieran una comprensión muy básica del contenido matemático para resolver y, sin embargo, sigan siendo muy desafiantes.
A modo de ejemplo que ilustre al mismo tiempo la construcción de conocimiento a través de la resolución de problemas y la atención a la diversidad desde un enfoque inclusivo, comentaremos una implementación de una actividad para introducir la mediatriz, la cual describe Arnal-Bailera (2013). La tarea, en lugar de comenzar explícitamente dando una definición de mediatriz, empieza dando un mapa en Geogebra y pidiendo al alumnado a colocar 5 o 6 puntos en el mapa que estén a la misma distancia de dos amigas (Ilustración 1). Es una tarea muy accesible que implica colocar un punto, medir distancias, observar y reflexionar. A pesar de que la actividad está pensada para primeros cursos de Educación Secundaria, podría plantearse en Educación Primaria, puesto que el “suelo” parte de ahí. Posteriormente, el andamiaje que se sucede en forma preguntas incidirá en qué figura se forma al unir esos puntos, en cuántos puntos son necesarios para encontrar todos, si fueran tres amigos qué pasaría, etc.
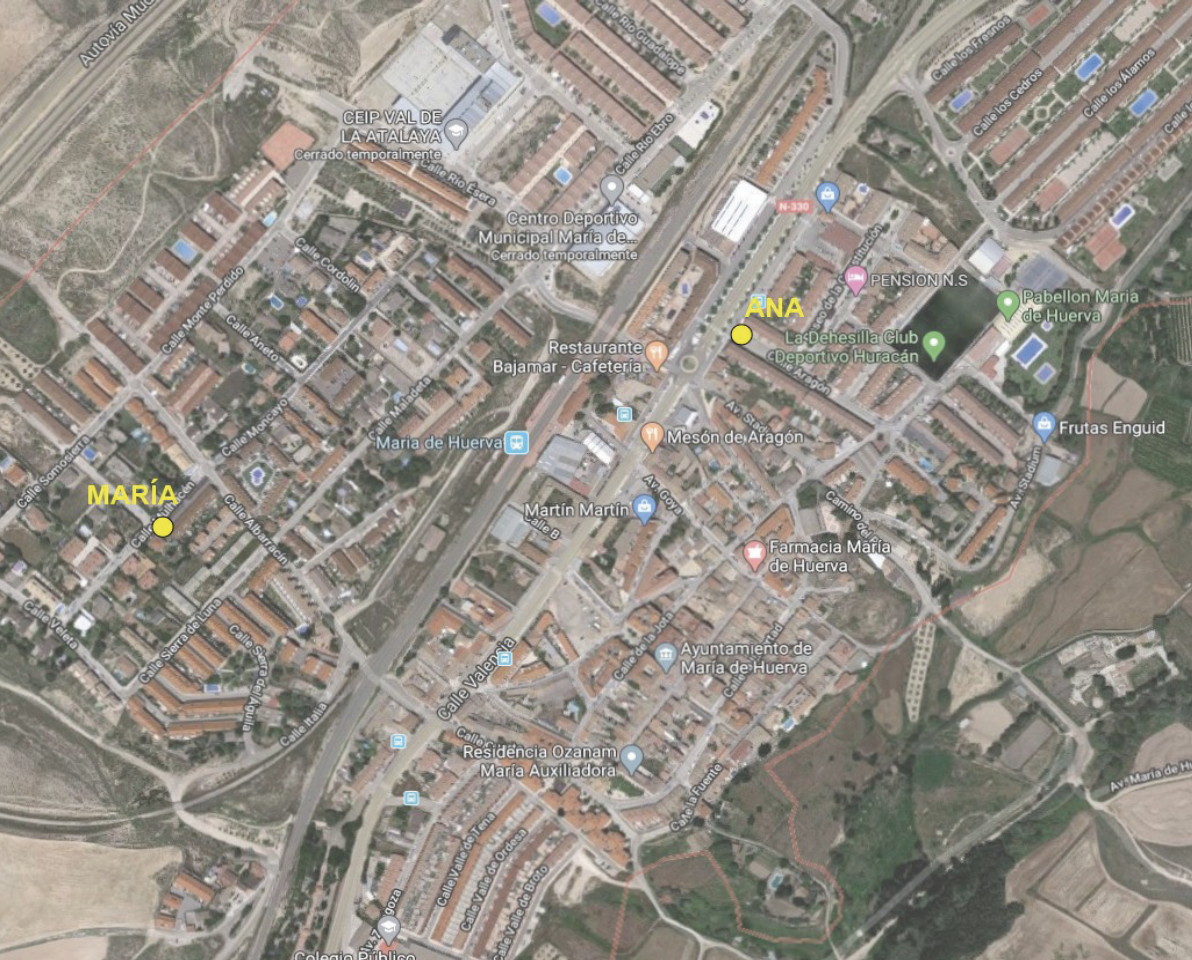
Ilustración 1: ¿Dónde podrán quedar estas dos amigas? Fuente: elaboración propia.
Conforme avanza la secuencia didáctica podemos identificar tareas que ejemplifican de forma especialmente clara cómo el aprendizaje, el conocimiento construido, no es el mismo para todos. Así, en una pregunta se trata de averiguar el circuncentro (punto de encuentro, en el contexto inicial) de algunos cuadriláteros y resulta que el del trapecio rectángulo no se puede encontrar (al trazar las mediatrices de los lados no se cortan en el mismo punto). Aquí es donde una alumna de 1º ESO realizó la observación de la Ilustración 2.
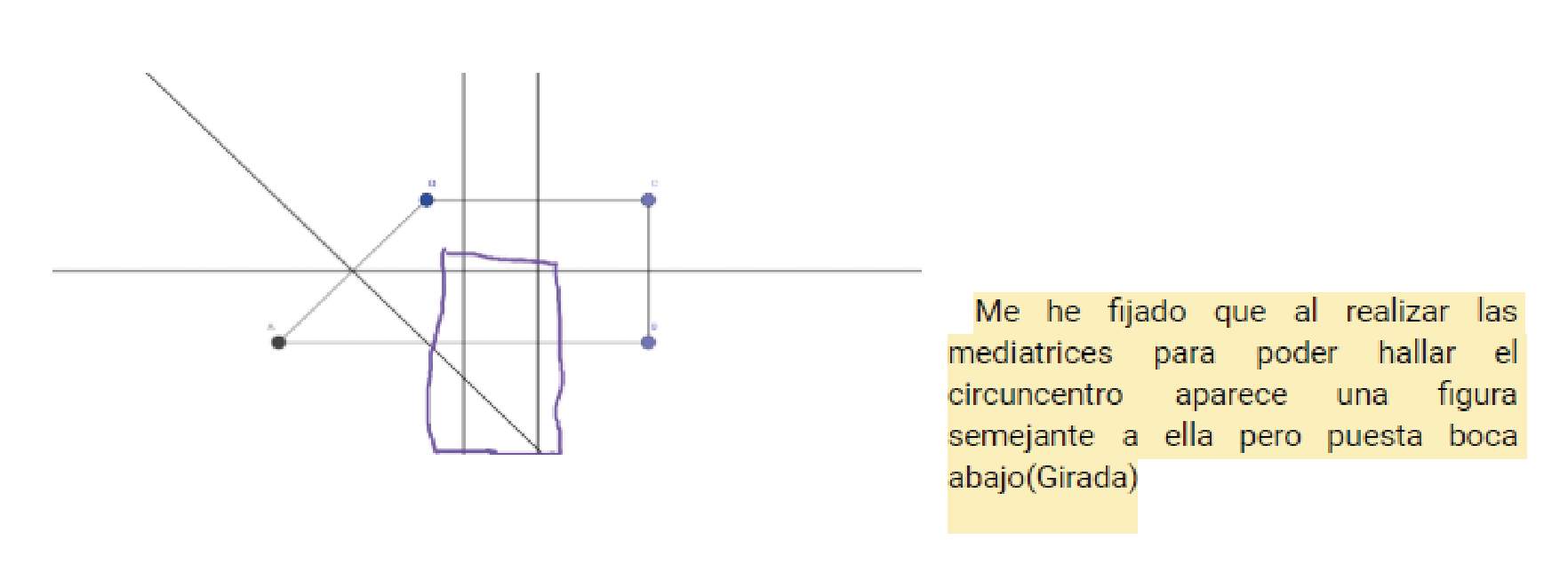
Ilustración 2: ¿Existe el circuncentro en un trapecio rectángulo? Fuente: elaboración propia.
La tarea no preguntaba por ello, pero la cultura de aula construida a lo largo del curso invitaba a explorar todos los caminos. El papel del docente es fundamental, pues debe darse cuenta de estas producciones y reaccionar en consecuencia. Aquí basta con preguntar cómo podía estar segura de lo que decía y que se animara a utilizar las herramientas de medida de GeoGebra para conjeturar (Ilustración 3). A continuación, se puede indagar por qué ocurre, lo que implica propiedades de la mediatriz y relaciones entre ángulos, así como aspectos de perpendicularidad, paralelismo y semejanza.
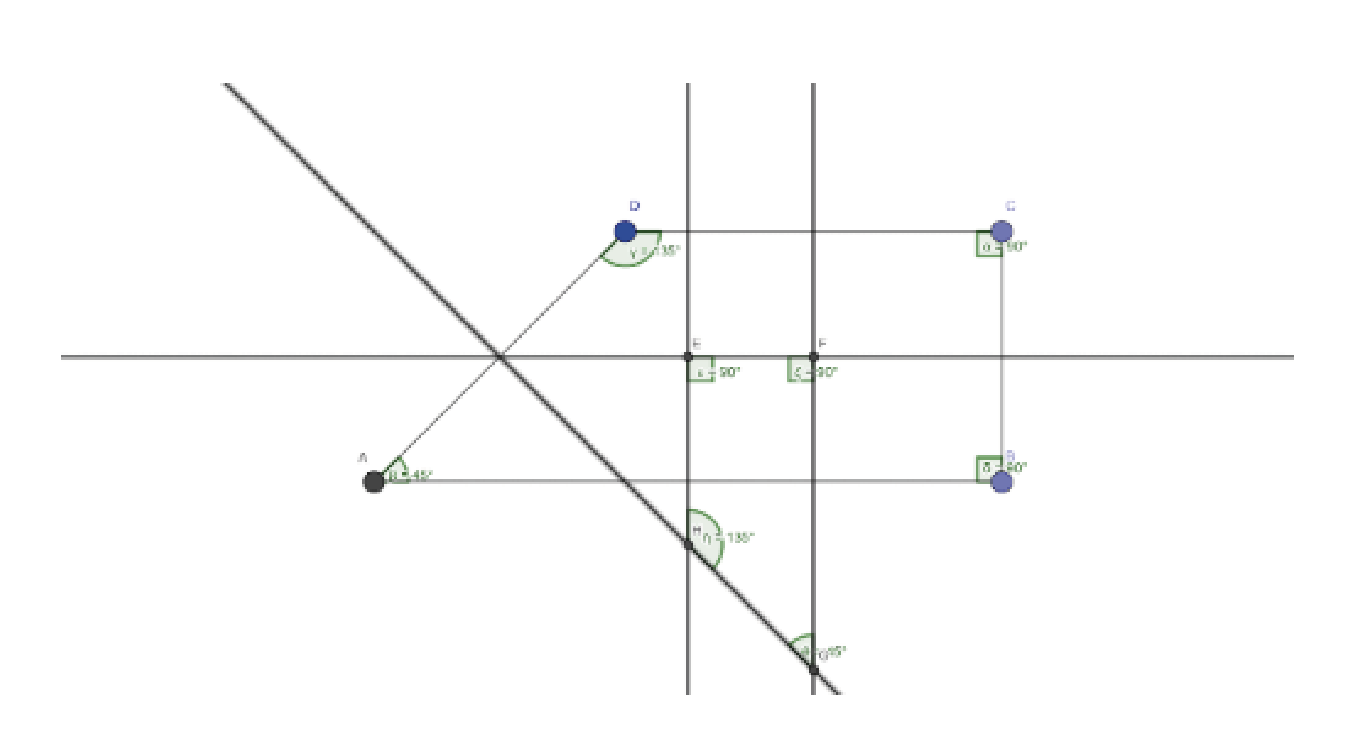
Ilustración 3: Ejemplo de producción de techo alto. Fuente: elaboración propia.
Los paralelismos que se aprecian en otras asignaturas son evidentes. En el aprendizaje de lenguas extranjeras, por ejemplo, la investigación didáctica señala la importancia del enfoque analítico. Este enfoque supone primero identificar una tarea relevante para el alumnado y analizarla para establecer las necesidades de este, de manera que pueda llevarla a cabo. Así se construyen los contenidos, el programa, de forma analítica y no a priori. Por el contrario, los enfoques que podemos denominar “tradicionales”, son sintéticos, pues construyen el programa seleccionando a priori unidades lingüísticas del sistema tal y como lo entiende el experto. El enfoque analítico se afianza con el enfoque del trabajo por tareas (Task-based approach to language teaching) a partir de los años 90 (Ellis, 2003) y está perfectamente alineado con la investigación en adquisición de lenguas extranjeras (Ellis y Shintani, 2014), así como con el enfoque orientado a la acción del MCER (Consejo de Europa, 2001, 2020) y su concepto de competencia comunicativa en términos de desempeño (“can do statements”) situado (en un contexto concreto, con una tarea concreta).
3.3. Planificación de los procesos de enseñanza y aprendizaje
La nueva estructura de los elementos curriculares y en particular la irrupción de las competencias específicas ha sembrado no pocas dudas en el profesorado sobre la forma en la que debe programarse la actividad docente. En este punto, creemos que son varios los factores que han generado esta incertidumbre, e incluso malestar entre el profesorado, ante la tarea de programar.
En primer lugar, no debemos obviar que la percepción general del profesorado sobre la programación didáctica es la de un documento de poca utilidad práctica cuya finalidad es cumplir un trámite administrativo y cubrir, eventualmente, al profesorado de un área o materia ante posibles reclamaciones.
En segundo lugar, el papel didáctico de las competencias específicas en las diferentes áreas de conocimiento no es uniforme. Tanto el encaje de las competencias específicas, como su recorrido histórico, como el nivel de implantación previo a la reforma curricular varía significativamente de unas materias a otras. Mientras que en algunas, como el aprendizaje de las lenguas extranjeras y las matemáticas, tienen un carácter marcado transversal respecto a los contenidos clásicos, en otras como las relacionadas con las ciencias experimentales y sociales, algunas competencias hacen referencia a partes específicas de los saberes básicos o implican procedimientos que hacen inviable que se puedan desarrollar con todos (o al menos con buena parte) de los saberes básicos, por ejemplo cunado se hace referencia al desarrollo de proyectos de investigación. Aun dentro de las que tienen un claro carácter transversal como en las lenguas extranjeras y las matemáticas su uso por el profesorado y, en general, su implantación en el sistema educativo tiene un recorrido diferente. En el caso de lenguas extranjeras, cuyas competencias específicas han sido claramente desarrolladas a partir del Marco Común Europeo de Referencia (MCER) (Consejo de Europa, 2001, 2020), no sorprende en ninguno de los colectivos que conforman la comunidad educativa que las evaluaciones se realicen a partir de competencias lingüísticas (reading, listening, etc.). Sin embargo, en el caso de las matemáticas, aunque ya hemos argumentado que tienen unos antecedentes sólidos y con un cierto recorrido histórico, ni la docencia habitual, ni evaluaciones como la EvAU/EVAU/EBAU, se centran en su desarrollo y evaluación.
Las diferencias apuntadas en el párrafo anterior hacen que lo que parezca lógico para programar en una materia, no lo sea en absoluto para otra. Por ejemplo, hay materias en las que puede tener sentido seleccionar un grupo de saberes básicos para desarrollar una competencia específica concreta, pero ¿tendría sentido en la enseñanza del inglés que se desarrollase la competencia comunicativa oral solo alrededor de unos contenidos concretos? ¿o sería deseable introducir en mayor medida situaciones en las que el alumnado tuviera que poner en juego dicha competencia comunicativa con los diferentes saberes básicos que se trabajan a lo largo del curso? Un caso similar lo podríamos ver en matemáticas con las competencias relacionadas con la resolución de problemas (aunque, en realidad con casi todas ellas). Si la resolución de problemas debe ser el eje conductor de la actividad matemática, no tendría sentido seleccionar, por poner un ejemplo, los saberes relacionados con las fracciones para resolver problemas. En cambio, el alumnado deberá desarrollar su competencia en la resolución de problemas alrededor de la mayor parte de los saberes básicos. Por otro lado, una competencia específica centrada en el desarrollo de un proyecto de investigación en un área relacionada con las ciencias experimentales bien podría trabajarse de forma única en un curso escolar seleccionando unos saberes básicos concretos a criterio del docente.
Por último, a todo lo expuesto anteriormente debemos sumar la falta de formación al profesorado centrada en las didácticas de las diferentes áreas de conocimiento. Una formación generalista, no puede abarcar las diferencias significativas entre áreas de conocimiento que ha supuesto la aparición de las competencias específicas en el currículo. Por tanto, el profesorado posee una formación muy limitada sobre este importante elemento curricular, en ocasiones incluso errónea al intentar homogeneizar la formación generalizando en el enfoque concreto de un área de conocimiento al resto.
A esta problemática para el diseño curricular de carácter general, se pueden añadir otros factores particulares del currículo desarrollado en las diferentes áreas de conocimiento. Por ejemplo volviéndonos a centrar en el caso de las matemáticas, hay aspectos curriculares que aparecen tanto dentro de las competencias específicas (y, por tanto, teóricamente, tienen un carácter de proceso) como dentro de los saberes básicos (y, por tanto, tienen un carácter de contenido sobre el que se generan actividades que desarrollan las competencias específicas), es el caso del pensamiento computacional y de los aspectos socioafectivos. Este hecho puede provocar no pocos problemas a la hora de programar e, incluso, de comprender las normas curriculares.
Las tensiones generadas entre el profesorado para la realización de las programaciones didácticas tampoco se pueden entender sin tener en cuenta que no solo irrumpe un nuevo elemento curricular, en ocasiones algo indefinido, en ocasiones muy desconocido, sino que, además, los criterios de evaluación dejan de mirar a los contenidos y se centran en el desarrollo de este nuevo elemento. Es decir, se debe evaluar la adquisición de las competencias específicas. Este último hecho, hace ineludible prestar una adecuada atención a cómo generar actividades de aula y de evaluación que pongan en juego las diferentes competencias específicas y a cómo integrar dichas competencias y los criterios de evaluación asociados en las programaciones didácticas.
Ante estas dificultades, se pueden dar pocas indicaciones de carácter general, salvo algunas que quizá puedan parecer obvias. En un primero momento, el profesorado podría inspeccionar cuidadosamente el currículo para distinguir aquellas competencias específicas y saberes básicos que tienen un claro carácter transversal, es decir, se pueden (o incluso deben) desarrollar durante todo el curso al trabajar los diferentes saberes básicos. Determinados procesos necesitan su desarrollo en diferentes momentos del curso e, idealmente, en todo momento del proceso de enseñanza y aprendizaje. Estos elementos curriculares transversales, no nos van a dar información sobre cómo secuenciar nuestra materia, por ejemplo, porque deben ser una constante en el proceso. Así, para generar nuestras unidades didácticas o de programación (la nomenclatura depende de la comunidad autónoma) secuenciarlas y temporalizarlas, tiene mucho más sentido fijarse en los elementos que no tienen ese marcado carácter transversal. Volviendo a los ejemplos de lenguas extranjeras y de matemáticas, por tanto, esa información sobre cómo generar ese primer esqueleto de nuestra programación que es la división en unidades más pequeñas, su orden y su duración, la vamos a encontrar de forma mucho más cómoda en los saberes básicos, que, en su mayor parte, no tienen ese carácter transversal.
Desde la afirmación anterior, caben hacer ciertas aclaraciones. En primer lugar, aunque para estructurar y secuenciar áreas como la de Matemáticas, tenga más sentido mirar hacia los saberes básicos esto no significa que se dejen de lado las competencias específicas. Todo lo contrario, ya que la actividad docente (y la evaluación en particular) debe dirigirse al desarrollo de las competencias específicas trabajando con los saberes seleccionados para cada unidad. Por otro lado, lo anterior tampoco debe entenderse como una invitación a compartimentar los contenidos, sin establecer relaciones internas y externas. De hecho, en áreas como la de matemáticas, el establecimiento de dichas relaciones forma parte de las competencias específicas. Debe, por tanto, repensarse la estructura de las unidades de forma que se generen oportunidades para conectar conocimientos, se dé cabida a la evaluación formativa durante todo el proceso de enseñanza y aprendizaje y, por supuesto, se proporcionen oportunidades para diseñar actividades que pongan en juego las competencias específicas.
En resumen, y volviendo a un ejemplo matemático, a pesar de algunas de las opiniones que se vierten en redes y en cursos de formación, tiene todo el sentido, por ejemplo, programar una unidad alrededor de “Las fracciones”. Sin embargo, aunque pudiera no apreciarse en la programación didáctica, el desarrollo de dicha unidad debe contemplar situaciones en las que se desarrollen las competencias específicas matemáticas alrededor de dicho contenido, lo que incluye oportunidades para conectar el tema principal de la unidad con otros elementos matemáticos y con sus uso y significados en otras disciplinas, por ejemplo.
El papel de las competencias específicas en este proceso de pensar cómo planificar es importante porque condiciona la búsqueda de una secuencia constructiva que permita que emerjan los saberes de las situaciones-problema.
3.4. Evaluación y calificación
La cuestión de la evaluación y, especialmente, de la calificación, en el marco de la LOMLOE ha sido objeto de críticas en claustros y redes sociales, debido a la burocracia que, aparentemente, requiere. Sin embargo, por un lado, el origen de estas críticas no hay que buscarlo en la LOMLOE, sino en los desarrollos curriculares de cada autonomía o, más concretamente, en las plataformas de gestión de cada administración. Por otro, habría que definir qué es burocracia y qué significa evaluar cierto criterio.
Resulta sencillo argumentar que la LOMLOE, per se, no añade carga de trabajo en este sentido, puesto que simplifica todo lo que tiene que ver con la evaluación. Si nos atenemos al número de “ítems evaluables”, el número de estándares de aprendizaje evaluables de la LOMCE excede de largo al de criterios de evaluación de la LOMLOE. Conviene observar que esta reducción de ítems no implica una evaluación más pobre, sino más rica, pues está centrada en los procesos que definen las competencias específicas. De hecho, como hemos mencionado, que los criterios de evaluación vayan asociados a competencias específicas es una novedad. También es un reto, puesto que si no se movilizan esas competencias en clase no tiene sentido evaluarlas.
Antes de adentrarnos en el marco de evaluación propuesto por la LOMLOE, es esencial aclarar ciertos conceptos, ya que la evaluación abarca diversas actividades con diferentes objetivos, y puede clasificarse según el momento de su realización y su propósito. Así, tenemos la evaluación inicial, continua y final. La evaluación inicial, usualmente de carácter diagnóstico, se realiza al inicio de un periodo de aprendizaje para determinar el nivel de conocimientos y habilidades previas del alumnado. La evaluación continua, de finalidad formativa y formadora, es un proceso que permite a los docentes monitorear el progreso del alumnado a lo largo del tiempo y proporcionar retroalimentación para que puedan mejorar el aprendizaje. La evaluación final se realiza al final de un período de aprendizaje con el objetivo de determinar si el alumnado ha logrado los objetivos de aprendizaje establecidos. Esta última se relaciona con la evaluación sumativa, que mide el rendimiento del alumnado al final de un período de aprendizaje. Aunque hemos resaltado el carácter formativo y formador de la evaluación continua, esto no quiere decir que el resto de los tipos de evaluación ignore el aprendizaje. Es más, podríamos decir que, si hablamos de educación, toda la evaluación debería servir para aprender, más que para diagnosticar.
Acudiendo a los currículos LOMLOE, se menciona el carácter integrador o global de Infantil, Primaria y ESO frente al carácter diferenciado propio de Bachillerato. La evaluación integradora o global busca evaluar el aprendizaje del alumnado en un contexto más amplio, teniendo en cuenta el desarrollo de habilidades y competencias interdisciplinarias. En cambio, la evaluación diferenciada se realiza de forma independiente según las áreas.
Existen otras clasificaciones de la evaluación, por ejemplo, según el agente que la realiza: evaluaciones de carácter interno o externo. Las primeras se realizan dentro de una misma institución, mientras que las segundas son llevadas a cabo por organismos o entidades externas a la institución, como puede ser el caso de pruebas estandarizadas nacionales o internacionales. Es el caso de las pruebas de acceso a la universidad. También, dentro de la propia institución la evaluación puede emanar de agentes diferentes, diferenciando entre autoevaluación, heteroevaluación y coevaluación.
Tanto los nuevos currículos LOMLOE como las orientaciones internacionales son muy claros en que la evaluación debe ser formativa. Esto significa que los indicios de aprendizaje que observamos y recogemos en el aula a partir de tareas que movilizan competencias específicas deben permitir al docente reaccionar en consecuencia y tomar decisiones. Se debería considerar, ante todo, el feedback que se proporciona al alumnado a partir de lo observado, para que pueda progresar en el aprendizaje y disponer de una oportunidad para construir su conocimiento con un nuevo andamiaje. Idealmente, este andamiaje debería ser diferenciado, lo cual quiere decir que depende de los indicios de aprendizaje observados y posibles dificultades que hayan emergido. En definitiva, los indicios posibilitan la toma de decisiones que condiciona el desarrollo de la secuencia didáctica.
Pero, ¿cómo llevar a la práctica este enfoque, que se podría denominar competencial, de la evaluación? Alsina (2018) sugiere un decálogo de ideas clave, que se sintetizan a continuación a partir de cuatro requisitos imprescindibles: 1) la evaluación forma parte del proceso de enseñanza-aprendizaje, por lo que debe ser coherente con el método de enseñanza (no tendría sentido, por ejemplo, enseñar matemáticas a través de la resolución de problemas y evaluarlas a través de un examen teórico); 2) la evaluación competencial sólo tiene sentido si se trabaja para desarrollar las competencias específicas, lo cual implica dejar de focalizarse únicamente en los saberes para poner el foco en dichas competencias; 3) la evaluación competencial requiere, a menudo, el uso de otros instrumentos como rúbricas, guías de orientación, etc.; 4) además de avaluar al alumnado desde una perspectiva formativa y formadora, es imprescindible avaluar la propia práctica y la riqueza competencial de las actividades. En Alsina et al. (2019) se expone un ejemplo de replanteamiento de la evaluación en un centro escolar a partir de estos principios.
En este escenario, una confusión habitual es confundir evaluación con calificación. Tanto, que en ocasiones se plantean dudas sobre evaluación que, en el fondo, son dudas sobre aspectos administrativos referentes a la calificación. De esta forma, nos encontramos con programaciones didácticas donde aparecen mezclados los criterios de evaluación con los criterios de calificación, cuando deberían ser apartados bastante independientes. De hecho, en la etapa de Educación Infantil las diferentes normativas contemplan un apartado de evaluación, pero no de calificación.
Es cierto que la administración es, en cierto modo, incoherente. Tanto la LOMLOE como sus desarrollos curriculares inciden mucho en la evaluación formativa. Sin embargo, al final de cada período evaluativo la administración exige un rendimiento de cuentas que obliga a sintetizar un proceso complejo —el de aprendizaje— en una calificación. La pérdida de información y, sobre todo, la posibilidad de que esa calificación sirva para progresar en el aprendizaje está fuera de toda duda. No obstante, el acto administrativo de calificar no debería condicionar todo el proceso de enseñanza y aprendizaje y, especialmente, no debería transformar este en una yincana de recolección de puntos. La calificación puede obtenerse a partir de los indicios de aprendizaje recogidos de diferentes maneras (Liljedahl, 2021).
De hecho, aunque la normativa no lo prohíbe, no son necesarios números en ningún momento. Los indicios pueden recogerse, para cada criterio, de forma cualitativa (por ejemplo, bajo, intermedio, avanzado) y, posteriormente, utilizar la mediana (en lugar de la media) para establecer el grado de desarrollo de cada uno de ellos y, al final, el de todas las competencias.
Quedaría por abordar cómo concretar los criterios de evaluación teniendo en cuenta los saberes que se movilizan. Esto no es algo para lo que exista una receta, puesto que depende, en primer lugar, de la naturaleza específica de cada materia y, en segundo lugar, del carácter de las competencias específicas. Así, hemos mencionado que hay asignaturas, como Matemáticas o Lengua extranjera, cuyas competencias son bastante independientes de los saberes (salvo excepciones, como una competencia en Matemáticas que alude al pensamiento computacional, que también aparece como saber básico), mientras que otras asignaturas tienen competencias muy ligadas a saberes básicos concretos.
Son las competencias específicas que hemos denominado transversales las que pueden causar más dudas, por la novedad. Sin embargo, basta con añadirles la concreción dada por el saber que se moviliza en una situación concreta. Veamos esto con el Criterio 2.1 de Matemáticas en Educación Primaria: “2.1 Seleccionar entre diferentes estrategias para resolver un problema, justificando la elección.” Será suficiente con concretar si se trata de problemas que involucran situaciones aditivas con números naturales, si son problemas de geometría, etc. El grado de desarrollo en cada caso puede venir dado por la complejidad de las tareas.
Por último, merece la pena dedicar unas líneas a otro debate: ¿hay que calificar todos los criterios de evaluación? La respuesta, ya que calificación y evaluación no son sinónimos, es clara: no. Puede haber criterios de evaluación que ayuden a proporcionar indicios de aprendizaje para ciertas competencias que no requieran de una calificación. Es el caso del eje competencial socioafectivo en Matemáticas, donde los indicios deben servir para tomar decisiones didácticas, pero una calificación podría ser, incluso, contraproducente. No obstante, las plataformas de gestión en cada comunidad condicionan todo esto ignorando o malinterpretando, en ocasiones, la propia normativa, pidiendo porcentajes concretos para cada criterio.
4. CONSIDERACIONES FINALES
En muchas ocasiones, los docentes mostramos cierta tendencia a plantear nuestras clases de la misma forma que experimentamos como estudiantes, atribuyéndole nuestro éxito, sin apenas considerar las directrices curriculares u otros factores. Esto conlleva una aceptación de la ideología dominante y supone importantes contradicciones entre las motivaciones y aspiraciones de los docentes al comienzo de sus carreras y la práctica real en los centros (Wright, 2017). En la misma línea, Gates (2006) describe cómo el bagaje social y cultural de los docentes moldea sus creencias pedagógicas. Esta inercia del sistema implica que un nuevo currículo, por sí solo, no va a suponer un cambio en la práctica de aula. Si así fuera, el cambio que promueve la LOMLOE no sería tal, puesto que la esencia de lo que persigue se puede rastrear en la LOGSE.
Desde esta perspectiva, en este artículo se ha indagado en torno a diferentes elementos cruciales de los currículos desarrollados al amparo de la LOMLOE (MEFP, 2022a, 2022b, 2022c, 2022d), con el propósito de profundizar en las relaciones de dichos elementos con las finalidades de la educación y reflexionar sobre lo que deberían suponer en la práctica docente. Para ello, una vez descritas dichas finalidades, se han abordado los principales organizadores curriculares: las competencias específicas y las situaciones de aprendizaje; el diseño de actividades y la metodología; la planificación de los procesos de enseñanza y aprendizaje; y la evaluación. Junto con un análisis de estos organizadores, se han aportado ejemplos desde diversas materias, con especial énfasis en la Matemática, para tratar de aportar algunos andamios que contribuyan a comprender las principales novedades de los currículos vigentes e incorporarlas en la práctica.
El primer organizador curricular al que se ha hecho referencia son las competencias específicas y las situaciones de aprendizaje, que son algunas de las principales novedades de los nuevos currículos y, a la vez, las que quizás han generado más confusiones en la práctica. Sobre las competencias específicas, se han destacado diversas ideas: son el marco para desarrollar las competencias clave, ofreciendo una concreción mucho mayor de qué es lo que se espera del alumnado para cada una de las materias al finalizar cada etapa (Beltrán-Pellicer y Alsina, 2022); su abordaje requiere identificar los saberes básicos de cada área y tomar decisiones sobre qué saberes se seleccionan para abordar las competencias específicas, considerando que el conjunto de saberes que se abordan durante un curso escolar debe haber cubierto las distintas competencias (Alsina, 2021); su nivel de desempeño se determina a través de los criterios de evaluación. Las situaciones de aprendizaje, de acuerdo con las directrices de la LOMLOE, son el marco a través del que se adquieren y desarrollan las competencias, por lo que, en la práctica, debemos planificar dichas situaciones con la mirada puesta en las competencias y su vinculación con los saberes, mientras que la gestión requiere necesariamente que llevemos a cabo una enseñanza de los saberes a través de las competencias (Alsina, 2021). Estas estrechas conexiones entre competencias y saberes tanto en la planificación como en la gestión de la enseñanza son fundamentales a lo largo de la escolaridad, pero la falta de coherencia entre el enfoque competencial que se propone en las diversas etapas se convierte en un obstáculo para conseguir las finalidades que plantea el currículo.
En el caso de Matemáticas, por ejemplo, existe una escasa conexión entre el carácter de las competencias en infantil, que se reducen prácticamente a lo numérico sin apenas hacer alusión a las competencias matemáticas de primaria (Alsina, 2022a): resolución de problemas, el razonamiento y la prueba, la comunicación y la representación y las conexiones. Como se ha mencionado, este es un grave problema interno de los currículos que, desde una perspectiva global, no ayuda a un tratamiento competencial longitudinal coherente a lo largo de las distintas etapas.
El segundo organizador curricular que se ha abordado ha profundizado en el diseño de actividades y la metodología. Asumiendo la gran diversidad de métodos, se ha puesto el foco en la importancia que tiene la enseñanza a través de la resolución de problemas para el aprendizaje del alumnado (Beltrán-Pellicer y Martínez-Juste, 2021), de manera que debería ser una especie de elemento transversal que condicione todo el currículo. A pesar de que cada asignatura debe acudir a su didáctica específica de referencia, nos encontramos con importantes paralelismos. Así, la construcción de significado en el aula debe comenzar desde las producciones del alumnado, sean problemas matemáticos o reflexiones en torno a una lectura. En este apartado metodológico, cabe insistir que, aunque desde la norma no se prohíba ninguna metodología explícitamente, aquellas con un fuerte componente expositivo no resultaran adecuadas para el desarrollo de las competencias específicas.
El tercer elemento en torno al cual se ha reflexionado es la planificación de los procesos de enseñanza y aprendizaje, es decir, la programación. Se ha puesto de manifiesto que se trata de un aspecto conflictivo porque, en la práctica, el profesorado lo consideramos poco útil, por lo que a menudo se convierte en un mero trámite, asociado a mucho trabajo que se podría dedicar a otras cuestiones que, desde la inmediatez, quizás son más necesarias. Sin embargo, en lugar de ser tratado como una carga burocrática, debería verse como el proceso de reflexión que fundamente el desarrollo del curso. En este proceso de reflexión, el profesorado debe concretar la conexión de los diferentes organizadores curriculares, en especial la conexión entre las competencias específicas (y los criterios de evaluación asociados a ellas) y los saberes básicos. La diferente naturaleza de las competencias específicas en cada disciplina conlleva que la materialización de esta conexión en las programaciones didácticas difiera sustancialmente entre áreas de conocimiento. Por tanto, es imprescindible que las administraciones educativas aborden la formación del profesorado de forma diferenciada, atendiendo a las diferentes didácticas específicas y no de forma global, o al menos, no solamente.
Finalmente, el cuarto y último organizador curricular abordado ha sido la evaluación, entendida como una parte más del proceso de enseñanza y aprendizaje. En este último elemento, se han desmitificado algunas críticas en torno a los criterios de evaluación, como por ejemplo su abundancia, y se ha hecho una distinción entre evaluación y calificación, destacando que quizás no todo puede ni debe ser calificado. Por ejemplo, en el caso de la Matemática, el sentido socioafectivo. Finalmente, se ha hecho hincapié en que el currículo enfatiza el papel formador de la evaluación. En ese sentido, el acto administrativo que supone la calificación puede relegarse a los momentos puntuales en que se exige.
En definitiva, pues, considerando el exceso normativo y algunos de los principales problemas que acarrea (de Azcárraga, 2022), en este artículo se ha tratado de separar el grano de la paja, para que el profesorado podamos distinguir las principales aportaciones de los nuevos currículos. Con los elementos descritos, se ha tratado de ayudar a conocer y comprender cuáles son los principales organizadores curriculares, reflexionar sobre ellos y disponer de herramientas para adaptarlos a nuestra práctica docente para mejorarla. Y todo ello, con el foco puesto en las grandes finalidades de la educación que, de modo muy sintético, es lo que pretenden los currículos.
REFERENCIAS
Alsina, Á. (2011). Educación matemática en contexto: de 3 a 6 años. ICE-Horsori.
Alsina, Á. (2018). La evaluación de la competencia matemática: ideas clave y recursos para el aula. Épsilon – Revista de Educación Matemática, 98, 7-23.
Alsina, Á. (2021). ¿Cómo definir una línea metodológica en el área de matemáticas?: Tomando decisiones en la escuela. Matemáticas, Educación y Sociedad, 4(2), 21-39.
Alsina, Á. (2018). La evaluación de la competencia matemática: ideas clave y recursos para el aula. Épsilon – Revista de Educación Matemática, 98, 7-23.
Alsina, Á. (2019). Itinerarios didácticos para la enseñanza de las matemáticas (6-12 años). Editorial Graó.
Alsina, Á. (2022a). Transformando el currículo español de Educación Infantil: la presencia de la competencia matemática y los procesos matemáticos. Números, Revista de Didáctica de las Matemáticas, 111, 33-48.
Alsina, Á. (2022b). Los contenidos matemáticos en el currículo de Educación Infantil: contrastando la legislación educativa española con la investigación en educación matemática infantil. Épsilon – Revista de Educación Matemática, 111, 67-89.
Alsina, Á. y Bosch, E. (2022). Numeración y cálculo en infantil y primaria: Diez materiales manipulativos esenciales para desarrollar el sentido numérico. TANGRAM – Revista de Educação Matemática, 5(3), 132-167. https://doi.org/10.30612/tangram.v5i3.16420
Alsina, Á., García, M. y Torrent, E. (2019). La evaluación de la competencia matemática desde la escuela y para la escuela. Unión, 15(55), 85-108.
Alsina, Á. y Rodríguez-Muñiz, L.J. (2021). Hilos de estadística y probabilidad en Twitter®: una nueva herramienta para el desarrollo profesional del profesorado de matemáticas. Educação Matemática Pesquisa, 23(4), 021-053. http://dx.doi.org/10.23925/983-3156.2021v23i4p001-007
Arnal-Bailera, A. (2013). Mediación tecnológica en la enseñanza y el aprendizaje de Geometría con grupos de riesgo: Estudio múltiple de casos. Manuscrito de Tesis Doctoral. UAB.Beltrán-Pellicer, p. y Alsina, Á. (2022). La competencia matemática en el currículo español de Educación Primaria. Márgenes, Revista de Educación de la Universidad de Málaga, 3(2), 31-58.
Beltrán-Pellicer, p. y Martínez-Juste, S. (2021). Enseñar a través de la resolución de problemas. Suma, 98, 11-21. https://bit.ly/3kZ9rzI
Brown, L. y Coles, A. (2013). On doing the same problem – first lessons and relentless consistency. En C. Margolinas (Ed.), Task design in mathematics education (Proceedings of the International Commission on Mathematical Instruction Study 22) (pp. 617-626). Springer.
Casey, K. y Sturgis, C. (2018). Levers and Logic Models: A Framework to Guide Research and Design of High-Quality Competency-Based Education Systems. iNACOL. https://bit.ly/3w0QeE9
CEMat (2021). Bases para la elaboración de un currículo de Matemáticas en Educación no Universitaria. https://bit.ly/3ytlGg1
Charles, R. (2005). Big ideas and understandings as the foundation for elementary and middle school mathematics. Journal of Mathematics Education Leadership, 7, 9-24.
Council of Europe. Council for Cultural Co-operation. Education Committee. Modern Languages Division (2001). Common European framework of reference for languages: Learning, teaching, assessment. Cambridge University Press.
Council of Europe (2020). Common European Framework of Reference for Languages: Learning, teaching, assessment – Companion volume. Council of Europe Publishing.
De Azcárraga, J. A. (2022). La nueva legislación educativa: por qué no mejorará la educación pública en España. Revista Española de Pedagogía, 80(281), 111-129.
Ellis, R. (2003). Task-based language learning and teaching. Oxford University Press.
Ellis, R. y Shintani, N. (2014). Exploring language pedagogy through second language acquisition research. Routledge
Fernández-Navas, M. (2015). Internet, organización en red y educ@ción: Estudio de un caso de buenas prácticas en Enseñanza Superior. Tesis doctoral. Universidad de Málaga. https://bit.ly/3sln7ZI
Gates, p. (2006). Going beyond Belief Systems: Exploring a Model for the Social Influence on Mathematics Teacher Beliefs. Educational Studies in Mathematics, 63(3), 347-369.
Godino, J. D. (2004). Didáctica de las Matemáticas para Maestros. Universidad de Granada. https://bit.ly/3NxfgSY
Ley Orgánica 8/2013, de 9 de diciembre, para la mejora de la calidad educativa. https://bit.ly/3Nhyytx
Ley Orgánica 3/2020, de 29 de diciembre, por la que se modifica la Ley Orgánica 2/2006, de 3 de mayo, de Educación. https://bit.ly/39NrMgQ
Liljedahl, p. (2021). Building Thinking Classrooms. Corwin.
Ministerio de Educación, Cultura y Deporte (MECD, 2014). Real Decreto 126/2014, de 28 de febrero, por el que se establece el currículo básico de la Educación Primaria. https://bit.ly/3yDUhYL
Ministerio de Educación y Formación Profesional (MEFP) (2022a). Real Decreto 95/2022, de 1 de febrero, por el que se establece la ordenación y las enseñanzas mínimas de la Educación Infantil. MEFp. https://bit.ly/3NVnkhu
Ministerio de Educación y Formación Profesional (MEFP) (2022b). Real Decreto 157/2022, de 1 de marzo, por el que se establecen la ordenación y las enseñanzas mínimas de la Educación Primaria. MEFp. https://bit.ly/3MWojuA
Ministerio de Educación y Formación Profesional (MEFP) (2022c). Real Decreto 217/2022, de 29 de marzo, por el que se establece la ordenación y las enseñanzas mínimas de la Educación Secundaria Obligatoria. MEFp. https://bit.ly/3MR6Bsu
Ministerio de Educación y Formación Profesional (MEFP) (2022d). Real Decreto 243/2022, de 5 de abril, por el que se establecen la ordenación y las enseñanzas mínimas del Bachillerato. MEFp. https://bit.ly/44d6W1S.
NCTM (2000). Principles and standards for school mathematics. NCTM.
Niss, M. (2002). Mathematical competencies and the learning of mathematics: the Danish Kom Project. Roskilde University.
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. Basic Books.
Polya, G. (1945). How to Solve It. Princeton University Press.
Singapore Ministry of Education (2018). 2020 secondary mathematics syllabuses. MOE.
Sullivan, P., Knott, L. y Yang, Y. (2015). The Relationships Between Task Design, Anticipated Pedagogies, and Student Learning. En: A. Watson y M. Ohtani, (Eds.) Task Design In Mathematics Education. New ICMI Study Series. Springer. https://doi.org/10.1007/978-3-319-09629-2_3
Toh, T.L. y Yeo, J.B.W. (2019). Big Ideas in Mathematics: Yearbook 2019. Association of Mathematics Educators. WSPC.
Van Den Heuvel-Panhuizen, M. (2005). The role of contexts in assessment problems in mathematics. For the learning of mathematics, 25(2), 2-23.
Wright, p. (2017) Critical relationships between teachers and learners of school mathematics. Pedagogy, Culture & Society, 25(4), 515-530. https://doi.org/10.1080/14681366.2017.1285345
