Recibido: 17 de mayo de 2022  Aceptado: 5 de julio de 2022  Publicado: 31 de julio de 2022
To cite this article: Beltrán-Pellicer, P. y Alsina, Á. (2022). La competencia matemática en el currículo español de Educación Primaria. Márgenes, Revista de Educación de la Universidad de Málaga, 3(2), 31-58. http://dx.doi.org10.24310/mgnmar.v3i2.14693
DOI: http://dx.doi.org10.24310/mgnmar.v3i2.14693

^*Pablo Beltrán-Pellicer 0000-0002-1275-9976. Universidad de Zaragoza (España). pbeltran@unizar.es
^**Ángel Alsina 0000-0001-8506-1838. Universitat de Girona (España). angel.alsina@udg.edu

Financiación: Investigación realizada como parte del proyecto de investigación PID2019-105601GB-I00 / AEI / 10.13039/501100011033, con apoyo del Grupo S60_20R-Investigación en Educación Matemática (Gobierno de Aragón y Fondo Social Europeo) y del proyecto de investigación 2020 ARMIF 00007 de la Agència de Gestió d’Ajuts Universitaris i de Recerca (AGAUR) de la Generalitat de Catalunya.

RESUMEN:
La reciente reforma curricular de Educación Primaria en España incorpora una serie de novedades que merece la pena analizar. Si bien el enfoque competencial no es nuevo, es la primera vez que se definen competencias específicas en cada materia. Esto es algo que aporta funcionalidad, ya que la generalidad de las competencias clave no resultaba práctica. En este artículo partimos, en primer lugar, de una revisión bibliográfica para delimitar el significado de “competencia matemática”. Posteriormente, analizamos su presencia en el currículo, tanto en los perfiles de salida que se configuran en relación con las competencias clave, como a través de las competencias específicas y sus criterios de evaluación. Igualmente, señalamos la relación de alguna de estas competencias específicas con los sentidos matemáticos, actuales “bloques de contenido”, pero más flexibles e interconectados. El análisis realizado ofrece una interpretación del nuevo currículo de matemáticas de Educación Primaria que puede resultar interesante para todo aquel que esté interesado en una visión de la enseñanza de las matemáticas a través de la resolución de problemas, el razonamiento y la prueba, la comunicación, las conexiones y la representación de las ideas matemáticas, considerando además el dominio socioafectivo y lo que ello implica. Al mismo tiempo, señalamos aquellos puntos que se prestan a confusión y elaboramos una crítica constructiva que abre nuevas líneas de investigación y que puede servir de inspiración para el último nivel de concreción curricular: los centros educativos.

PALABRAS CLAVE: competencia matemática; procesos matemáticos; sentido matemático; currículo, educación matemática; didáctica de la matemática; Educación Primaria

ABSTRACT:
The recent curricular reform of Primary Education in Spain incorporates several changes that need to be analysed. Although the competence approach is not new, it is the first time that specific competences have been defined for each subject. This change provides functionality, since the generality of the key competences was not practical. In this article we start by drawing a literature review to delimit the meaning of "mathematical competence". Then, we analyse its presence in the curriculum, both in the stage profiles that are configured in relation to the key competencies, and through the specific competencies and their evaluation criteria. In addition, we point out the relationship of some of these specific competences with the mathematical senses, current "content blocks", but more flexible and interconnected. The analysis carried out offers an interpretation of the new primary mathematics curriculum that may be interesting for anyone who is interested in an approach to teaching mathematics through problem solving, reasoning and proof, communication, connections and representation of mathematical ideas, also considering the socio-affective domain and what it implies. At the same time, we point out those aspects that may result confusing and we elaborate a constructive critic that opens new lines of research, hoping that may serve as inspiration for the last level of curricular specification: educational centres.

KEYWORDS: mathematical competence; mathematical processes; mathematical sense; curriculum; mathematics education; didactics of mathematics; primary education

1. INTRODUCCIÓN

A finales del siglo pasado, en el seno de The Organisation for Economic Cooperation and Development (OECD), cuya misión es diseñar mejores políticas para una vida mejor, se produjo un intenso debate acerca de cómo se debía orientar la educación del siglo XXI teniendo en cuenta que las sociedades actuales demandan que los individuos se enfrenten a la complejidad de muchas áreas de sus vidas. Este profundo proceso de análisis, reflexión y proyección sobre cómo debía transformarse la educación lo ganó el enfoque competencial y, en consecuencia, surgió el Proyecto de Definición y Selección de Competencias (DeSeCo) de la OECD, cuyo principal objetivo era proporcionar un marco conceptual sólido que estableciese los objetivos que debía alcanzar cualquier sistema educativo que pretendiera fomentar la educación a lo largo de toda la vida (Rychen et al., 2001; Rychen y Salganik, 2003; Salganik et al., 1999). En el marco de este proyecto, se consideró que “una competencia es más que conocimientos y destrezas. Involucra la habilidad de enfrentar demandas complejas, apoyándose en y movilizando recursos psicosociales (incluyendo destrezas y actitudes) en un contexto en particular” (OECD, 2005, p. 3). A pesar de que la idea de definir los aprendizajes en términos de competencias fue impulsada por la OECD, no es algo exclusivo de esta organización (Fernández-Navas, 2015, pp. 187-188). Organismos como la International Association for K-12 Online Learning (iNACOL), por ejemplo, llevan mucho tiempo trabajando también en sistemas de educación basados en competencias (Casey y Sturgey, 2018).

Desde entonces, el enfoque competencial se ha ido introduciendo con mayor o menor fortuna en los currículos de la mayoría de los países. En el caso de la legislación educativa española de Educación Primaria, que es la etapa educativa en la que se focaliza este artículo, las competencias básicas se incorporan por primera vez en el Real Decreto 1513/2006, de 7 de diciembre, por el que se establecen las enseñanzas mínimas de la Educación Primaria. En este documento, se considera que las competencias básicas:

[...] permiten identificar aquellos aprendizajes que se consideran imprescindibles desde un planteamiento integrador y orientado a la aplicación de los saberes adquiridos. Su logro deberá capacitar a los alumnos y alumnas para su realización personal, el ejercicio de la ciudadanía activa, la incorporación a la vida adulta de manera satisfactoria y el desarrollo de un aprendizaje permanente a lo largo de la vida. (p. 3)

El Real Decreto 126/2014, de 28 de febrero, por el que se establece el currículo básico de la Educación Primaria (MECD, 2014), se hace eco de la Recomendación del Parlamento Europeo y del Consejo, de 18 de diciembre de 2006, sobre las competencias clave para el aprendizaje permanente. De esta manera, el término “competencias básicas” desaparece y, en su lugar, se utiliza “competencias clave” o simplemente “competencias”. Se define como sigue:

Competencias: capacidades para aplicar de forma integrada los contenidos propios de cada enseñanza y etapa educativa, con el fin de lograr la realización adecuada de actividades y la resolución eficaz de problemas complejos. (p. 4).

En el Real Decreto 157/2022, de 1 de marzo, por el que se establecen la ordenación y las enseñanzas mínimas de la Educación Primaria (MEFP, 2022a) se distinguen las competencias clave y las competencias específicas, que se conceptualizan de la forma siguiente:

2. Competencias clave: desempeños que se consideran imprescindibles para que el alumnado pueda progresar con garantías de éxito en su itinerario formativo, y afrontar los principales retos y desafíos globales y locales. Las competencias clave aparecen recogidas en el Perfil de salida del alumnado al término de la enseñanza básica y son la adaptación al sistema educativo español de las competencias clave establecidas en la Recomendación del Consejo de la Unión Europea, de 22 de mayo de 2018 relativa a las competencias clave para el aprendizaje permanente (p. 6).
3. Competencias específicas: desempeños que el alumnado debe poder desplegar en actividades o en situaciones cuyo abordaje requiere de los saberes básicos de cada área o ámbito. Las competencias específicas constituyen un elemento de conexión entre, por una parte, el Perfil de salida del alumnado, y, por otra, los saberes básicos de las áreas o ámbitos y los criterios de evaluación (p. 6).

Se observa, pues, que en las diversas versiones del currículo español la idea de competencia se va modificando: primero, se vincula a aprendizajes, seguidamente a capacidades y, en la última versión, a desempeños, lo cual pone de manifiesto que se trata de un concepto dinámico, en constante evolución y difícil de definir.

Paralelamente a este proceso de conceptualización, se han ido definiendo también las diversas competencias. El programa PISA de la OECD, por ejemplo, cuyo objetivo es evaluar las habilidades, la pericia y las aptitudes de los estudiantes cuando llegan al final de la etapa de enseñanza obligatoria para analizar y resolver problemas, para manejar información y para enfrentar situaciones que se les presentarán en la vida adulta y que requerirán de tales habilidades, tiene el valor de haber expandido a nivel internacional tres tipos de competencias, sin desmerecer el resto: competencia lectora, competencia matemática y competencia científica.

La competencia matemática, que es el objeto de análisis de nuestro estudio, se conceptualiza inicialmente en el marco de la OECD como una capacidad individual para identificar y comprender el papel que desempeñan las matemáticas en el mundo, hacer juicios fundados y usar e implicarse con las matemáticas en aquellos momentos que se presenten necesidades para su vida individual como ciudadano constructivo, comprometido y reflexivo. (OECD, 2003, p. 24)

Más adelante, ya desde PISA 2012 y también en PISA 2015, se amplía la definición:

la capacidad de un individuo para formular, emplear e interpretar matemáticas en una variedad de contextos. Incluye el razonamiento matemático y el uso de conceptos, procedimientos, hechos e instrumentos matemáticos para describir, explicar y predecir fenómenos. Ayuda a los individuos a reconocer el papel que desempeñan las matemáticas en el mundo y a tomar los juicios y las decisiones fundamentadas que necesitan los ciudadanos constructivos, comprometidos y reflexivos. (OECD, 2018, p. 75)

La competencia matemática está explícitamente presente en los respectivos decretos españoles de Educación Primaria desde 2006, aunque de diversas formas en función de la conceptualización asociada al término de competencia.

Mientras que la competencia matemática y la competencia en el conocimiento y la interacción con el mundo físico eran dos de las competencias básicas de la Ley Orgánica 2/2006, de 3 de mayo, de Educación (LOE), a partir de la Ley Orgánica 8/2013, de 9 de diciembre, para la mejora de la calidad educativa (LOMCE) aparecen integradas en la Competencia matemática y competencias básicas en ciencia y tecnología. En la Ley Orgánica 3/2020, de 29 de diciembre, por la que se modifica la Ley Orgánica 2/2006, de 3 de mayo, de Educación (LOMLOE) se añade el término ingeniería, al pasar a denominarse Competencia matemática y competencia en ciencia, tecnología e ingeniería. No obstante, en lo que se refiere a las evaluaciones de diagnóstico, se menciona la competencia matemática de manera aislada (LOMLOE, art. 144):

La finalidad de esta evaluación será diagnóstica y en ella se comprobará al menos el grado de dominio de la competencia en comunicación lingüística y de la competencia matemática.

En este sentido, el objetivo de este artículo es revisar la presencia de la competencia matemática en el currículo español vigente de Educación Primaria, el Real Decreto 157/2022, para determinar qué aporta el enfoque competencial a la enseñanza de las matemáticas. Así mismo, se pretende ofrecer algunas orientaciones al profesorado interesado en introducir este enfoque de enseñanza en el aula.

2. LA COMPETENCIA MATEMÁTICA

Alsina (2019) subraya que la implantación de un currículo orientado a la adquisición de la competencia matemática en Educación Primaria significa un paso adelante y pretende formar personas con un mayor grado de eficacia para afrontar los problemas reales que plantea la vida, más allá de los estrictamente académicos. Para profundizar en este enfoque competencial, se sintetizan las principales aportaciones de diversos organismos y autores como el NCTM (2003), Niss (2002) o la OECD (2003).

2.1. La competencia matemática según el Consejo Nacional de Profesores de Matemáticos de Estados Unidos (NCTM, 2000)

Esta asociación, constituida principalmente por profesores de matemáticas de Educación Infantil, Primaria y Secundaria, así como por investigadores en educación matemática, ha establecido los estándares de contenidos para Números y operaciones, Álgebra, Geometría, Medida, y Análisis de datos y Probabilidad. Estos estándares describen explícitamente los contenidos que se deberían aprender de los 3 a los 18 años. De la misma forma, también definen estándares de procesos (Resolución de problemas, Razonamiento y prueba, Comunicación, Conexiones y Representación), que ponen de relieve las formas de adquisición y uso de dichos contenidos (NCTM, 2000).

A partir de la publicación de estos estándares, los currículos de matemáticas de muchos países han ido incorporando paulatinamente los procesos matemáticos que, junto con los contenidos matemáticos, constituyen el conjunto de conocimientos matemáticos que favorecen la competencia matemática. Conviene observar que, en estos principios y estándares, el término “competencia” no se operativiza de la misma manera que los marcos que mencionaremos en los siguientes apartados. Aquí aparece de forma casual en la introducción, sin definirla de forma explícita:

Mathematical competence opens doors to productive futures. A lack of mathematical competence keeps those doors closed. NCTM challenges the assumption that mathematics is only for the select few. (NCTM, 2000, p. 5)

A lo largo del documento, el término competencia vuelve a aparecer con la intención de separar conceptos y competencias; es decir, logos y praxis. En la Ilustración 1 se muestra la interrelación entre contenidos y procesos a partir de la cual emerge, de manera pragmática, la noción de competencia en el documento del NCTM (2000).

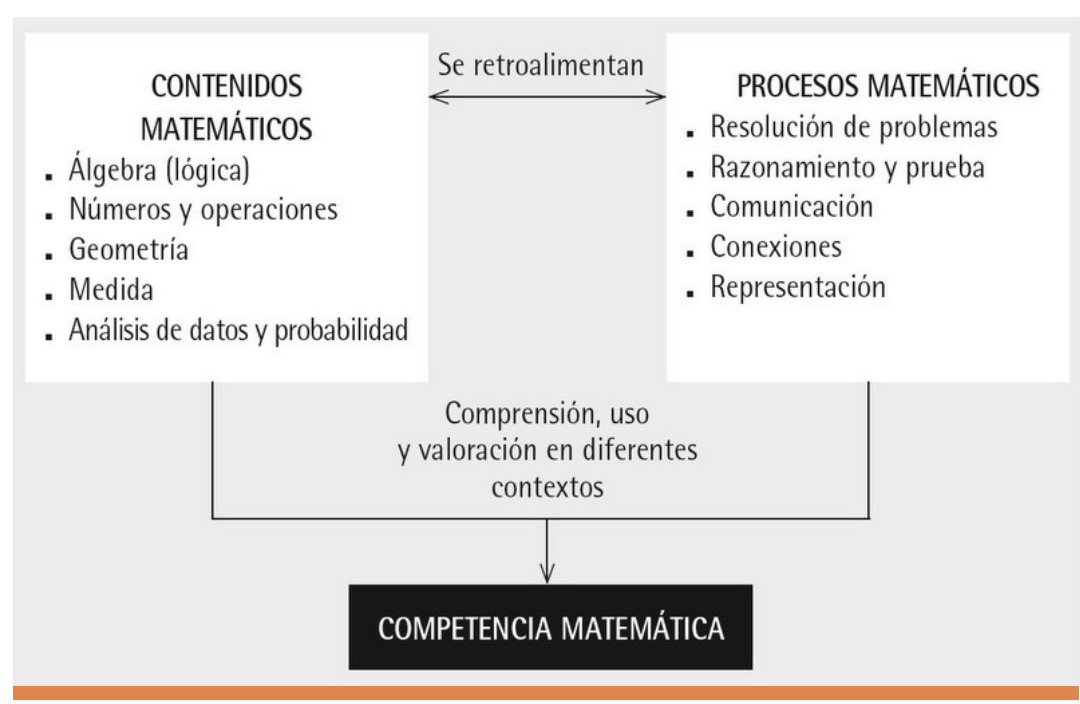
Ilustración 1. Interrelación entre contenidos y procesos matemáticos en los principios y estándares del NCTM (2000). Fuente: Alsina (2019, p. 20)

Este planteamiento curricular, de acuerdo con Alsina (2012), implica partir de un enfoque mucho más globalizado que no se limite a trabajar de manera lineal los contenidos matemáticos por bloques, sino trabajarlos de forma integrada con los procesos, explorando cómo se potencian y usándolos sin prejuicios. Adicionalmente, exige trabajar para favorecer la autonomía mental del alumnado, potenciando la elaboración de hipótesis, las estrategias creativas de resolución de problemas, la discusión, el contraste, la negociación de significados, la construcción conjunta de soluciones y la búsqueda de formas para comunicar planteamientos y resultados. En definitiva, pues, se trata de ayudar, a través de los procesos de pensamiento matemático, a gestionar el conocimiento, las habilidades y las emociones para conseguir un objetivo a menudo más cercano a situaciones funcionales y en contextos de vida cotidiana que a su uso académico.

2.2. La competencia matemática según Mogen Niss (Niss, 2002)

Paralelamente a los planteamientos del NCTM, en el marco del proyecto danés de definición de las competencias y el aprendizaje de las matemáticas, se señala la necesidad de substituir los currículos de matemáticas orientados a la adquisición de contenidos, ya que se centran exclusivamente en la adquisición de símbolos y de técnicas, por currículos orientados al uso significativo de estos contenidos en una variedad de situaciones en las que las matemáticas pueden desempeñar un papel. Desde esta perspectiva, Niss (2002) define la competencia matemática como la habilidad para comprender, juzgar, hacer y usar las matemáticas en una variedad de contextos y situaciones en las que las matemáticas juegan o pueden desempeñar un papel. Este autor propone un total de ocho competencias matemáticas que clasifica en dos grupos (Tabla 1).

Tabla 1. Competencias matemáticas (Niss, 2002, pp. 7-9)

Estas ocho competencias tienen que ver con procesos mentales o físicos, actividades y comportamientos y, por lo tanto, Niss (2002) aclara que se centran en lo que las personas pueden hacer. Más adelante, Alsina (2021) amplía esta idea aclarando que el enfoque competencial de las matemáticas se focaliza en lo que las personas pueden pensar y hacer, y describe cinco prácticas productivas para avanzar en esta dirección, asumiendo que una práctica productiva es “una acción o destreza educativa útil y provechosa para promover el aprendizaje de las matemáticas con sentido en todos los niveles” (p. 2).

2.3. La competencia matemática según la Organización para la Cooperación y el Desarrollo Económico (OECD, 2003)

A partir de la conceptualización ya indicada, en el marco del Proyecto PISA se concretan ocho competencias (Tabla 2).

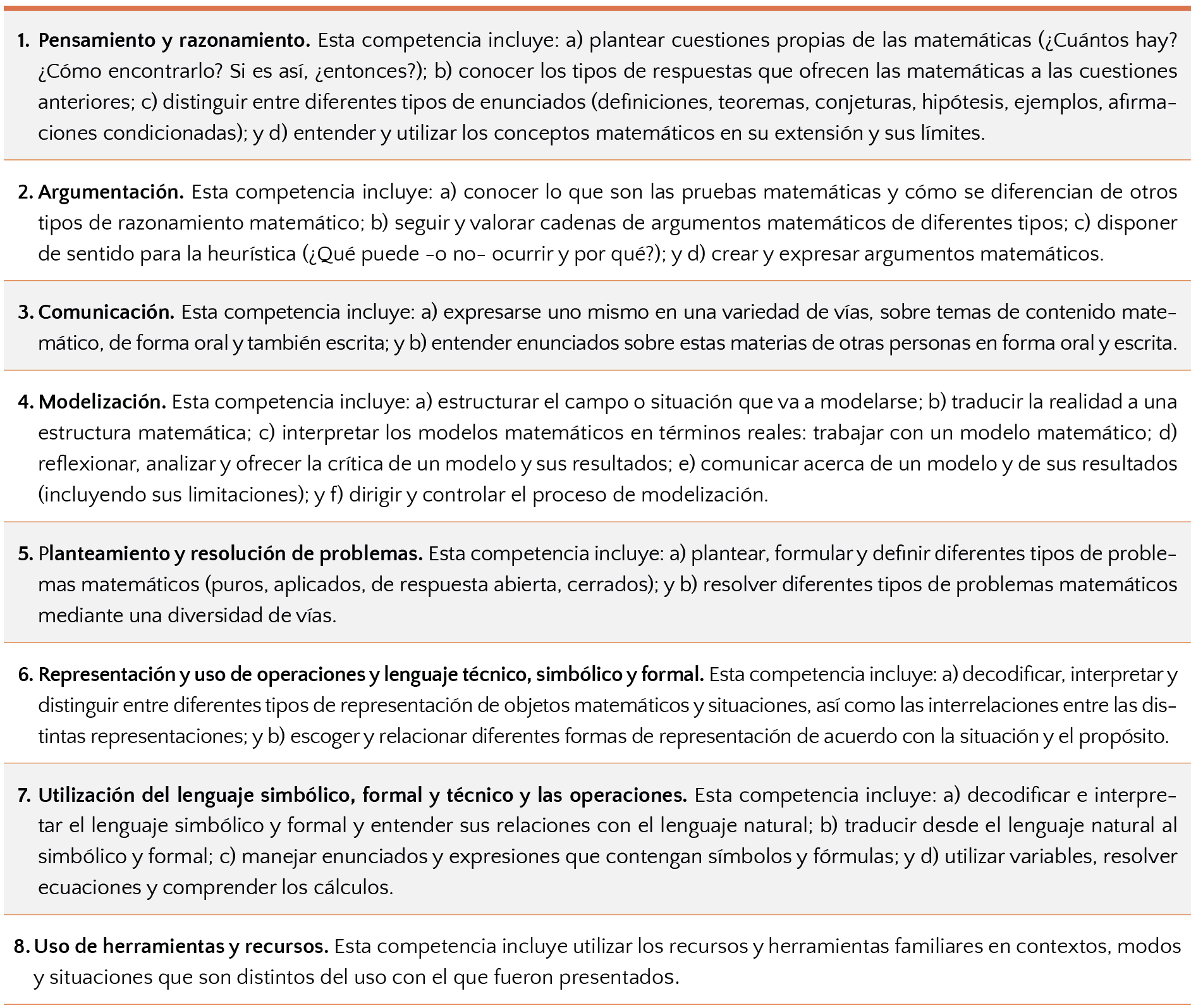
Tabla 2. Competencias matemáticas (OECD, 2003, pp. 40-41)

A partir de un análisis comparativo entre las tres aproximaciones al término competencia matemática, se observan diversas similitudes (Tabla 3).

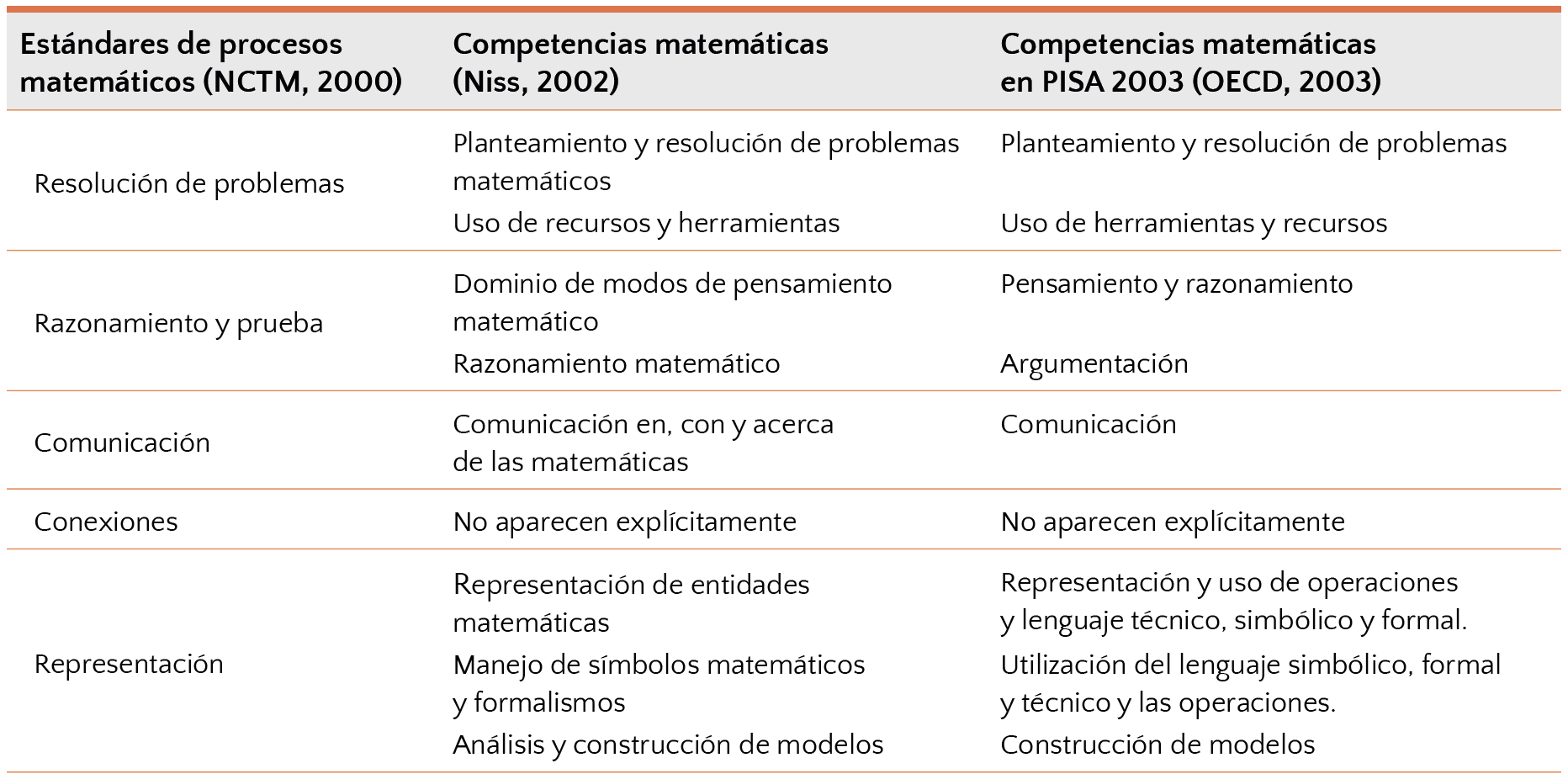
Tabla 3. Comparación entre los estándares de procesos y las competencias matemáticas (Alsina, 2019, p. 25)

De acuerdo con Alsina (2019), los procesos matemáticos y las competencias matemáticas enfatizan una misma idea: la capacidad de usar de forma comprensiva y eficaz las matemáticas que se aprenden en la escuela en una variedad de contextos, además del escolar, reforzando de esta forma un enfoque social en torno al diseño, aplicación y evaluación de situaciones de aula que fomenten el aprendizaje matemático.

De forma más concreta, a partir del análisis comparativo realizado, concluye que, para aprender matemáticas desde este enfoque social, es imprescindible fomentar la adquisición de las competencias matemáticas siguientes:

• Pensar matemáticamente: construir conocimientos matemáticos a partir de situaciones en las que tengan sentido, experimentar, intuir, relacionar conceptos y realizar abstracciones.
• Razonar matemáticamente: realizar deducciones e inducciones, particularizar y generalizar; argumentar las decisiones tomadas, así como la lección de los procesos seguidos y de las técnicas usadas.
• Plantearse y resolver problemas: leer y entender el enunciado, generar preguntas relacionadas con una situación problemática, planificar y desarrollar estrategias de resolución y verificar la validez de las soluciones.
• Obtener, interpretar y generar información con contenido matemático.
• Usar las técnicas matemáticas básicas (para contar, operar, medir, situarse en el espacio y organizar y analizar datos) y los instrumentos (calculadoras y TIC, de dibujo y de medida) para hacer matemáticas.
• Interpretar y representar expresiones, procesos y resultados matemáticos con palabras, dibujos, símbolos, números y materiales.
• Comunicar el trabajo y los descubrimientos a los demás, tanto oralmente como por escrito, usando de forma progresiva el lenguaje matemático.
  
  

3. LA COMPETENCIA MATEMÁTICA EN EL CURRÍCULO ESPAÑOL: ANÁLISIS DE SU PRESENCIA Y EJEMPLOS DE IMPLEMENTACIÓN EN EL AULA

3.1. La competencia matemática como competencia clave

En el Real Decreto 157/2022, la competencia matemática se considera una competencia clave que se ha integrado dentro de la competencia STEM (por sus siglas en inglés), junto con la competencia en ciencia, tecnología e ingeniería. Esta competencia “entraña la comprensión del mundo utilizando los métodos científicos, el pensamiento y representación matemáticos, la tecnología y los métodos de la ingeniería para transformar el entorno de forma comprometida, responsable y sostenible” (p. 21). Este enfoque, que ya se puso de manifiesto en Europa con la publicación del informe Europe needs more Scientists en el inicio del siglo XXI (European Comission, 2004), es una novedad en el currículo español y responde a una reclamación que desde hace muchos años vienen realizando investigadores, formadores y docentes en educación científico-tecnológica y matemática con una postura crítica. Este colectivo lamenta que la atención por la educación STEAM se ha focalizado en el interés gubernamental, empresarial y social en mejorar la cantidad, la calidad y diversidad de los profesionales SMET, STEM o STEAM para garantizar el progreso económico y social deseable, dejando de lado la alfabetización científico-tecnológica y matemática de toda la ciudadanía. Desde este punto de vista, la incorporación de este enfoque integrado en el currículum contribuye a promover la alfabetización en el ámbito STEAM para todos los estudiantes como un valor personal en sí mismo, con el propósito de proporcionarles herramientas que les permitan identificar y aplicar, tanto los conocimientos clave como las formas de hacer, pensar, hablar y sentir de la ciencia, la ingeniería, la tecnología, las artes y la matemática, de forma más o menos integrada, para comprender, decidir y/o actuar ante problemas complejos y para construir soluciones creativas e innovadoras, aprovechando las sinergias personales y las tecnologías disponibles, y de forma crítica, reflexiva y con valores (Couso, 2017).

Considerando este enfoque integrado, en el Decreto 157/2022 se indica, en un primer momento, que “la competencia matemática permite desarrollar y aplicar la perspectiva y el razonamiento matemáticos con el fin de resolver diversos problemas en diferentes contextos” (p. 21). Más adelante, en este mismo decreto, se amplía esta definición y se señala que

la alfabetización matemática, es decir, la adquisición de los conocimientos, las destrezas y actitudes, así como los instrumentos necesarios para aplicar la perspectiva y el razonamiento matemáticos en la formulación de una situación-problema, seleccionar las herramientas adecuadas para su resolución, interpretar las soluciones en el contexto y tomar decisiones estratégicas. Esta comprensión de las matemáticas ayudará al alumnado a emitir juicios fundamentados y a tomar decisiones, destrezas estas imprescindibles en su formación como ciudadanos comprometidos y reflexivos capaces de afrontar los desafíos del siglo XXI. (p. 92)

En cambio, en el Real Decreto 95/2022, de 1 de febrero, por el que se establecen la ordenación y las enseñanzas mínimas de la Educación Infantil, la competencia matemática (también integrada dentro de la competencia STEM) se asocia a la iniciación de destrezas lógico-matemáticas, que se focalizan en la iniciación temprana en habilidades numéricas básicas (pp. 11-12). Esta divergencia conceptual puede dificultar la transición entre ambas etapas: por un lado, en Educación Infantil la competencia matemática se focaliza en lo numérico, ofreciendo una visión sesgada de la educación matemática infantil y sus finalidades; y, por otro lado, en Educación Primaria se vincula a la resolución de problemas, a pesar de que parece que se asocia más a un medio para obtener soluciones que para aprender matemáticas, en el sentido planteado por Beltrán-Pellicer y Martínez-Juste (2021) cuando se refieren a enseñar a través de la resolución de problemas.

Otra cuestión relevante son los descriptores operativos de la competencia STEM, en los que la competencia matemática tiene una presencia explícita. Son dos de los cinco descriptores, STEM1 y STEM4, que se recogen en la Tabla 4.

Tabla 4. Descriptores operativos de la competencia STEM vinculados explícitamente a la competencia matemática en el Decreto 157/2022 (p. 21)

El descriptor STEM1 es específicamente matemático, refiriéndose a la utilización del razonamiento matemático para resolver problemas. Si comparamos la redacción del descriptor propio de la Educación Primaria con el de la Enseñanza Básica veremos que son muy similares. Ahora bien, ¿por qué parafrasear lo mismo de dos maneras? ¿Acaso analizar críticamente las soluciones obtenidas no es lo mismo que reflexionar sobre las soluciones? ¿Qué diferencia hay? Por otro lado, ¿por qué hablar de razonamiento matemático en situaciones conocidas? ¿Son los problemas una de estas situaciones conocidas? Creemos que estas diferencias en la redacción son innecesarias, pudiendo haber sido sustituidas por un descriptor único de la competencia y unas breves orientaciones acerca de cómo los saberes de cada etapa condicionan y matizan el desarrollo de la competencia.

En cuanto al descriptor STEM4, el foco está en los procesos de interpretación y de comunicación de todas las disciplinas a las que se refiere el acrónimo STEM, incluidas, de forma explícita, las matemáticas. De nuevo nos encontramos con diferencias en la redacción del descriptor para Primaria y para la Básica, todas ellas menores salvo que en la Básica se menciona el papel del lenguaje matemático-formal para compartir y construir conocimiento. ¿A qué se refiere con “formal”? ¿Expresiones algebraicas? Si así fuera, ¿no se considera también los signos “+” y “-” para la suma y para la resta como una formalización de la operación para resolver ciertas situaciones aditivas? Cuando menos, resulta confuso porque en los formatos de presentación de la información se alude a los “símbolos” en ambas etapas, mientras que, en la lista de ejemplo, aparecen las “fórmulas” en la de la Básica.

Además de los descriptores STEM1 y STEM4, que claramente aluden a las matemáticas, podría llegar a interpretarse que la competencia matemática podría tener cierta cabida también en el STEM2 y en el STEM3. No obstante, para ello habría que realizar cierto esfuerzo de exégesis. De esta forma, dirigiendo nuestra mirada al STEM2, podríamos preguntarnos si el pensamiento matemático forma parte del pensamiento científico (a priori, no, ya que son letras diferentes en STEM). O, ya en el STEM3, ¿cómo deben ser esos proyectos para que las matemáticas tengan cabida y repercusión en ese producto final?

Shaughnessy (2012, 2013), durante los años en que fue presidente del NCTM, alertaba sobre el peligro de dilución de la M de Matemáticas dentro de lo STEM. La manera de plantear los descriptores operativos del Decreto 157/2022 podría contribuir a ello puesto que, si bien se produce un intento de definirlos en términos integrados en el marco de STEM, por un lado, algunos indicadores se focalizan exclusivamente en una de las disciplinas, mostrando en realidad una segregación entre ellas más que una integración real que las enriquezca mutuamente; y, por otro lado, en aquellos descriptores que tratan de integrar disciplinas, no se hacen referencias explícitas a las peculiaridades de cada una.

Por lo tanto, en el caso concreto de las Matemáticas, el problema tiene su origen en que los objetos que se construyen en esta disciplina se usan también en otras materias, pudiendo dar la impresión de que hacer matemáticas es solo hacer cuentas en contextos diversos. La construcción de esos objetos no es algo trivial, como tampoco lo es el establecimiento de conexiones entre ellos. Procesos como la modelización son esencialmente distintos en el aprendizaje de matemáticas y en experimentales. En matemáticas, la modelización de un fenómeno físico o de las acciones que se realizan con un manipulable persigue abstraer un objeto matemático, construirlo o conectarlo con otros objetos. Por el contrario, la modelización en ciencias experimentales trata de emplear un objeto matemático ya construido para comprender y extraer nueva información de un fenómeno físico, realizar predicciones, etc. Es cierto que hay cierto solapamiento inevitable en el que los contextos extra-matemáticos nos llevan a resolver problemas del mundo físico en matemáticos, mostrando los usos de los objetos matemáticos y extender su fenomenología. Sin embargo, es fundamental reconocer la importancia de la construcción de los objetos y su comprensión en profundidad. Y eso forma parte de los procesos de enseñanza y aprendizaje de las matemáticas.

3.2. Las competencias específicas asociadas a la competencia matemática

En el Real Decreto 157/2022 se considera que las competencias específicas asociadas a las matemáticas se relacionan entre sí constituyendo un todo integrado, y se organizan en cinco ejes fundamentales: resolución de problemas, razonamiento y prueba, conexiones, comunicación y representación, y destrezas socioafectivas.

Como puede observarse, los cuatro primeros ejes incluyen los procesos matemáticos del NCTM (2000). Adicionalmente, se incluyen las destrezas socioafectivas y, en su conjunto, “orientan sobre los procesos y principios metodológicos que deben dirigir la enseñanza y el aprendizaje de las matemáticas y favorecen el enfoque interdisciplinar y la innovación” (p. 92). Se propone evaluar estas competencias específicas “a través de la puesta en acción de diferentes saberes, proporcionando la flexibilidad necesaria para establecer conexiones entre ellos” (p. 93). Dichos saberes se estructuran en torno al concepto de sentido matemático, organizados en dos dimensiones: cognitiva y afectiva. Los diferentes sentidos están formados por una serie de saberes que integran conocimientos, destrezas y actitudes: sentido numérico, sentido de la medida, sentido espacial, sentido algebraico, sentido estocástico y sentido socioafectivo.

Ya que en la propia normativa no se define de forma explícita qué se entiende por sentido matemático, recurrimos al documento del CEMAT (2021) (p. 13):

Entendemos el sentido matemático como el conjunto de capacidades relacionadas con el dominio en contexto de contenidos numéricos y algebraicos, geométricos, métricos y estocásticos, que permiten emplear estos contenidos de una manera funcional y con confianza en las propias habilidades (Ruiz-Hidalgo et al., 2019). El origen de esta consideración arranca de apreciar que las matemáticas son una ciencia cultural, que permite pensar, entender y actuar en los problemas del entorno que tienen que ver con la cantidad, la forma, el tamaño y la incertidumbre aleatoria. Esta idea permite dar coherencia y continuidad al paso de Primaria a Secundaria al tiempo que plantea una enseñanza funcional de las matemáticas, que haga predominar y dar sentido a los conceptos en resolución de problemas o tareas en contexto, frente al aprendizaje de destrezas o algoritmos en situaciones descontextualizadas. (Rico y Díez, 2011)

Otro elemento curricular que permite concretar la idea de competencia son los criterios de evaluación. Estos, a diferencia de leyes anteriores, se definen específicamente para cada competencia, separados completamente de los sentidos (antiguos contenidos). La propia normativa indica que no existe una correspondencia unívoca y directa entre los criterios de evaluación y los saberes. Es más, señala que las competencias se han de evaluar a través de la puesta en acción de diferentes saberes, de forma flexible y estableciendo conexiones entre ellos. Resulta llamativo que, siendo criterios competenciales, aparezcan desglosados por ciclos. Es decir, entendemos que un proceso (p. ej., la resolución de problemas), es el mismo, independientemente de si estamos construyendo las fracciones en tercer ciclo o de si estamos abordando situaciones aditivas en primer ciclo. Como veremos, esto conduce a que prácticamente cambien algunas palabras entre ciclo y ciclo, y a ciertas incoherencias, añadiduras u omisiones sin mayor razón de ser. No obstante, esto puede ser debido a que se ha querido mantener el mismo marco de diseño curricular para todas las materias, habiendo otras en las que, quizá, encaje más la diferenciación de criterios competenciales por ciclos.

En lo que sigue, se abordan los cinco ejes a partir de los que se organizan las competencias específicas. Cada sección sigue la misma estructura: en primer lugar, se presenta una descripción de la competencia específica fundamentada en la literatura previa; en segundo lugar, se revisa su presencia en el decreto 257/2022; y, finalmente, se muestran ejemplos y o contraejemplos, es decir, actividades implementadas competenciales y/o no competenciales.

3.2.1. Resolución de problemas

Un aspecto importante es que se ha querido recoger en la normativa curricular la importancia que tiene el proceso de resolución de problemas. En particular, el papel que debe cumplir como medio para el aprendizaje:

La resolución de problemas, que constituye el primero de los ejes mencionados, se debe favorecer no solo como competencia específica del área, sino como método para su aprendizaje.

No obstante, esto choca con que la primera frase del encabezado señale el marcado carácter instrumental de las matemáticas, en lugar de comenzar resaltando su valor en sí mismas y como herencia cultural, cosa que hace después. Esta tensión entre la instrumentalidad y el valor intrínseco de las matemáticas con su propio modo de pensamiento se identificaba ya en los descriptores operativos de la competencia STEM, donde se integra, de alguna manera, la competencia matemática. De los cinco descriptores, las matemáticas solamente aparecen de forma explícita en el descriptor STEM1, que es específico de matemáticas, y en el STEM4, de forma integrada con otras áreas.

Las dos competencias específicas del eje de resolución de problemas son las siguientes (p. 102):

CE.M1. Interpretar situaciones de la vida cotidiana, proporcionando una representación matemática de las mismas mediante conceptos, herramientas y estrategias, para analizar la información más relevante.

CE.M2. Resolver situaciones problematizadas, aplicando diferentes técnicas, estrategias y formas de razonamiento, para explorar distintas maneras de proceder, obtener soluciones y asegurar su validez desde un punto de vista formal y en relación con el contexto planteado.

La CE.M1 pone el foco en los procesos de interpretación y análisis de las situaciones, mientras que la CE.M2 se centra en el proceso de resolución. Al igual que en currículos anteriores, observamos en este un abuso de la expresión “vida cotidiana”, lo cual puede dar lugar a malinterpretaciones. ¿Cuál es la vida cotidiana del alumnado? ¿Todo el alumnado tiene la misma vida cotidiana? Quizá hubiese sido más preciso hablar de situaciones realistas, imaginables o significativas para el alumnado, en el sentido en que lo hacen Van den Heuvel-Panhuizen y Drijvers (2013), lo cual no implica que sean situaciones del “mundo real”.

Es interesante que en la descripción de la CE.M1 se señalen aspectos de la resolución de problemas que tradicionalmente han llevado a confusión. Por ejemplo, un problema no tiene por qué venir dado siempre en forma de enunciado verbal escrito, sino que puede encontrar su origen en un mensaje verbal oral, un dibujo, un gráfico, etc. Se echa en falta, quizá porque en el ámbito de la investigación en educación matemática y las sociedades de profesores hay consenso en ello, una mayor concreción de lo que es un problema. Una confusión habitual fuera de esos entornos es considerar problema a un ejercicio con contexto. No obstante, aunque no se profundice explícitamente en esta cuestión, el resto del currículo permite dotar de significado al término problema (igual que al término competencia).

Vistas en conjunto las competencias específicas, se identifican las fases del modelo de resolución de Polya: comprensión del enunciado, planificar una estrategia, ejecutarla y revisar y reflexionar sobre la solución. Conviene señalar que no debe caerse en la típica malinterpretación de este modelo, aplicando técnicas rutinarias consistentes en identificar datos, elegir una operación y escribir la solución, que es una manera reduccionista de presentar la resolución de problemas en muchos libros de texto, principalmente.

Los criterios de evaluación quedan recogidos en la Tabla 5. Esencialmente, se distinguen dos criterios para la CE.M1, uno referido a la comprensión de las preguntas planteadas y otro referido a la producción de representaciones que ayuden a la resolución de las situaciones-problema. Aquí, el término representación ha de entenderse en sentido amplio, ya que en el primer ciclo se menciona los manipulativos como medio de representación. Es extraño que no se mencionen los manipulativos en el criterio análogo para segundo y tercer ciclo.

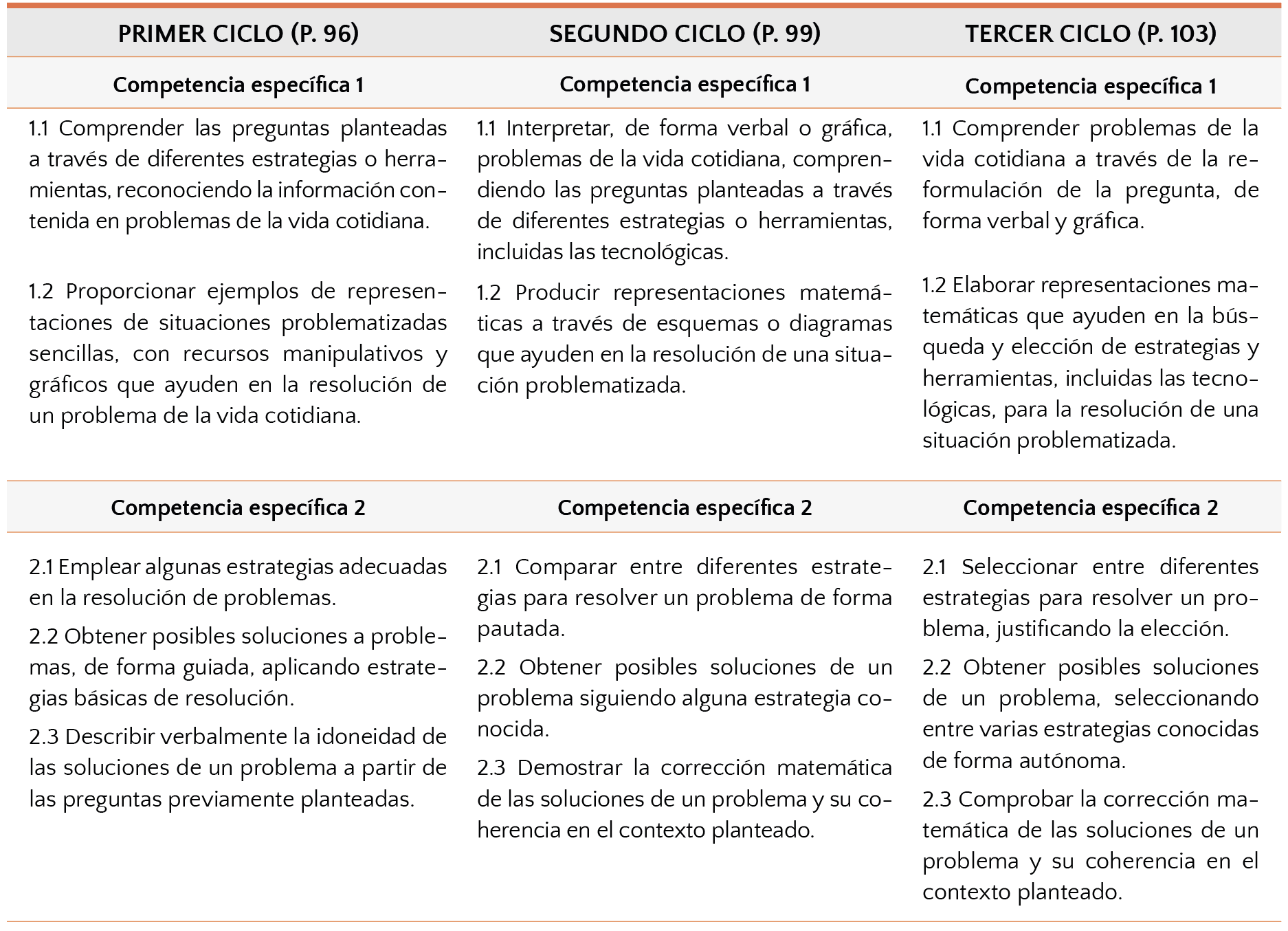
Tabla 5. Criterios de evaluación de las competencias del eje de resolución de problemas

En la organización de los criterios de evaluación del eje de resolución de problemas por ciclos, al tratarse en realidad de un proceso que tiene una continuidad a lo largo de la etapa, se observan algunas incoherencias, sobre todo en el uso del lenguaje. Estas incoherencias pueden inducir al profesorado a interpretaciones incorrectas acerca de lo que es y lo que implica resolver problemas. Por ejemplo, respecto a las estrategias de resolución de problemas (2.2.), se usa “emplear”, “comparar” y “seleccionar” respectivamente, pero ¿acaso no sería más adecuado mencionar en todos los ciclos, por igual, que el alumnado debe pensar estrategias y elegir la más adecuada con base en los conocimientos que movilizan? ¿cómo puede emplearse una estrategia si antes no se ha pensado? o ¿cómo pueden compararse o seleccionarse sin antes haberlas pensado?; en la obtención de soluciones (2.3) se explicita que debe hacerse “de forma guiada” únicamente en el primer ciclo, pero quizás la recomendación que sería más oportuna es que esto depende de los saberes puestos en juego en cada ciclo. Finalmente, en la valoración de las soluciones, se utiliza “describir”, “demostrar” y “comprobar” respectivamente, cuando en matemáticas, demostrar requiere el uso de teoremas o axiomas que el alumnado de estas edades todavía no moviliza. Quizás se podría haber precisado si lo que se pretende realmente es que el alumnado haga una demostración informal, aunque quizás es más propio de estas edades hacer comprobaciones con base en la propia experiencia.

3.2.2. Razonamiento y prueba

Las dos competencias específicas del eje de razonamiento y prueba son las siguientes:

CE.M3. Explorar, formular y comprobar conjeturas sencillas o plantear problemas de tipo matemático en situaciones basadas en la vida cotidiana, de forma guiada, reconociendo el valor del razonamiento y la argumentación, para contrastar su validez, adquirir e integrar nuevo conocimiento.

CE.M4. Utilizar el pensamiento computacional, organizando datos, descomponiendo en partes, reconociendo patrones, generalizando e interpretando, modificando y creando algoritmos de forma guiada, para modelizar y automatizar situaciones de la vida cotidiana.

Observamos que la competencia CE.M3 recoge, por un lado, la necesidad de que el alumnado desarrolle la capacidad de explorar, formular y comprobar conjeturas. Es decir, debe afrontar situaciones en las que no esté claro el camino a seguir y ser capaz de expresar su razonamiento. Además, la comprobación de la validez de esos razonamientos y de las conclusiones a las que llegue, deben ir más allá de “está bien” o “está mal”. Es importante, y así lo establece el descriptor de la competencia, que esa reflexión conlleve la integración de nuevo conocimiento o el establecimiento de conexiones en la red personal de significados del alumnado. Por otro lado, la CE.M3 señala explícitamente que el alumnado debe aprender a plantear problemas. La invención de problemas (problem posing) es una actividad que ha dado lugar a toda una línea internacional de investigación (Felmer et al., 2016). Ejemplifica de forma excelente el aspecto creativo de las matemáticas y tiene un gran valor porque exige que el alumnado reinterprete la red de conocimientos y competencias procedentes de situaciones de aprendizaje anteriores.

Una novedad del currículo es la entrada del pensamiento computacional, tanto como competencia específica de Matemáticas (CE.M4) como conjunto de saberes. Realmente, a pesar de lo extendido del término, resulta complicado definir con claridad qué es exactamente el pensamiento computacional y cuál es su relación con las matemáticas. La expresión “pensamiento computacional” fue introducida por Papert (1980), creador del lenguaje de programación Logo. Más adelante, fue retomada por Wing (2006) quien definió pensamiento computacional como el modo en que piensa un científico de datos, señalando que es una habilidad básica de la que se puede beneficiar todo el mundo, al mismo nivel que la lectura, la escritura y la aritmética. Más recientemente, autores como Shute, et al. (2017) lo han definido como el marco conceptual necesario para resolver problemas de forma efectiva y eficiente; es decir, algorítmicamente (con o sin la ayuda de ordenadores), cuyas soluciones puedan ser transferibles a otros contextos. Weintrop, et al. (2016), ante la vaguedad de algunas definiciones y la falta de consenso realizaron una revisión de la literatura y desarrollaron un proyecto para elaborar una exhaustiva taxonomía de prácticas propias del pensamiento computacional. Dicha taxonomía se compone de cuatro categorías de prácticas: datos, modelizado y simulación, resolución computacional de problemas y análisis de sistemas.

La relación de las matemáticas con la computación es doble y tiene una larga historia. Por un lado, las ciencias de la computación permiten abordar problemas propios de las matemáticas y, por otro lado, desde el pensamiento computacional es posible revisitar ciertos conceptos de las matemáticas desde otro punto de vista. Además, el proceso de resolución de problemas en matemáticas y el proceso de resolución computacional presentan ciertas semejanzas. El reconocimiento de patrones, la descomposición del problema en otros más simples, la búsqueda de generalizaciones y abstracciones, la importancia de la modelización son elementos comunes a ambos. Sin embargo, no son los únicos, pues también podemos considerar aspectos afectivos y de carácter metacognitivo, como el desarrollo de una actitud de perseverancia, aprendizaje a través del ensayo y error, flexibilidad, etc.

Ahora bien, a pesar de estos puntos en común, pensamiento matemático y pensamiento computacional no son lo mismo y tampoco puede concebirse el uno como subconjunto del otro (Yadav y Berthelsen, 2021). Si no se desarrollan, a modo de ejemplo, situaciones de aprendizaje que ilustren diferentes maneras de abordar el pensamiento computacional en Matemáticas, puede caerse en el error de considerar únicamente actividades triviales con robots o tecnología educativa. De hecho, a veces tiende a pensarse que programación y pensamiento computacional es lo mismo. La programación es la escritura de código que pueda ser interpretado por un ordenador para realizar una serie de acciones, mientras que el pensamiento computacional se relaciona más con la resolución de problemas, es un modo de pensamiento. Especialmente, conviene tener presente que el pensamiento computacional puede desarrollarse sin necesidad de la tecnología.

Resulta interesante que los saberes propios del pensamiento computacional se engloben dentro del sentido algebraico. Se indica, textualmente, que es por “razones organizativas” (MEFP, 2022a, p. 101), cuando se podía haber aludido a que es el sentido donde más claras son las conexiones. Un objeto clásico y, en cierto sentido, controvertido, del currículo de matemáticas son los algoritmos de las operaciones. Tradicionalmente han sido incluidos en el bloque de dedicado a la aritmética (bloque de Números, en el anterior currículo). Países como Suecia los eliminaron, en su momento, del currículo, para volver a incluirlos posteriormente, pero dentro del bloque de contenidos algebraicos (Bråting, 2021; Kilhamn y Bråting, 2019). Este desplazamiento implica un cambio claro de objetivos de aprendizaje alrededor de los algoritmos de las operaciones. No se trata de automatizar nada, sino de comprender, crear, adaptar y optimizar algoritmos, al mismo tiempo que se establecen relaciones y se exploran propiedades del sistema de numeración.

De nuevo, nos encontramos con un intento de graduación de los criterios de evaluación de estas competencias a lo largo de los ciclos. De esta forma, en la Tabla 6 vemos que en primer ciclo se trata de “realizar” conjeturas de forma “guiada”, mientras que en segundo y tercer ciclo hay que “analizar” de forma “pautada”. En primer lugar, siempre hay un andamiaje –o debe haberlo– en las situaciones de aprendizaje, lo cual no quiere decir que haya que decir explícitamente qué hacer exactamente en cada momento. En segundo lugar, ¿cuál es la diferencia entre guiar y pautar? Entre realizar y analizar está claro que hay una diferencia, pero ¿para qué lanzar –realizar– una conjetura si luego no se contrasta –analiza– de alguna manera? El proceso es el mismo a lo largo de los tres ciclos, y las únicas distinciones que podrían llevarse a cabo tendrían que ver con el carácter intuitivo o informal de una conjetura y el carácter riguroso de una prueba. No obstante, las implicaciones de esta articulación entre la prueba y la conjetura se extienden hasta bachillerato.

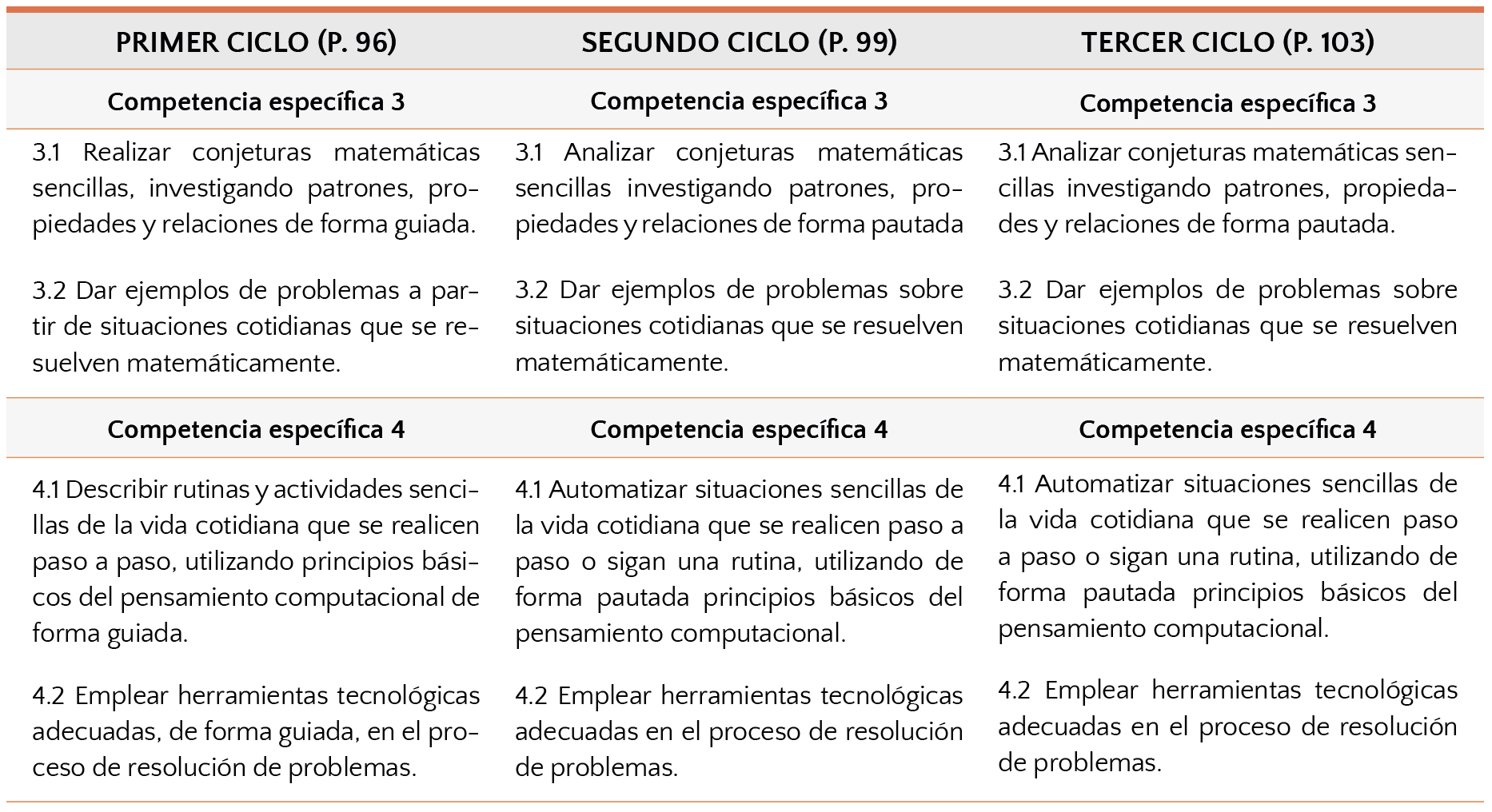
Tabla 6. Criterios de evaluación de las competencias del eje de razonamiento y prueba

3.2.3. Conexiones

La competencia específica del eje de conexiones es la siguiente:

CE.M5. Reconocer y utilizar conexiones entre las diferentes ideas matemáticas, así como identificar las matemáticas implicadas en otras áreas o en la vida cotidiana, interrelacionando conceptos y procedimientos, para interpretar situaciones y contextos diversos.

Una lectura global del currículo revela una clara intención de que los aprendizajes vayan más allá de una recopilación de hechos y procedimientos. Aunque las matemáticas no son una colección de saberes aislados, se suelen presentar compartimentadas por «ramas de conocimiento». Tradicionalmente, en el currículo de las diferentes leyes educativas en España esto se ha traducido en los diferentes bloques de contenido. Ahora, en cambio, se han configurado en lo que se denomina sentidos matemáticos (numérico, medida, espacial, algebraico y computacional y estocástico). La idea es que son unos “bloques” más permeables y flexibles. De ahí la importancia de establecer conexiones entre las diferentes ideas, dentro y fuera de las matemáticas, dando lugar a un aprendizaje más significativo, profundo y duradero. Además, de esta manera se subraya la naturaleza de las matemáticas como herencia cultural.

En la Tabla 7 recogemos los criterios de evaluación del eje de conexiones. Puede decirse que hay uno dedicado al establecimiento de conexiones intra-matemáticas (5.1) y otro a las extra-matemáticas (5.2). A lo largo de los ciclos, cambia ligeramente la redacción, pero los procesos tienden a ser los mismos, si bien las conexiones interdisciplinares –que son la razón de ser del enfoque integrado STEM o STEAM– se mencionan únicamente en el primer ciclo, mientras que en los dos ciclos restantes se enfatizan los vínculos entre las matemáticas y la vida cotidiana, pero no se hace mención explícita a las relaciones entre las matemáticas y otras disciplinas para promover un enriquecimiento mutuo.

Tabla 7. Criterios de evaluación de la competencia de conexiones

3.2.4. Comunicación y representación

La competencia específica del eje de comunicación y representación es la siguiente:

CE.M6. Comunicar y representar, de forma individual y colectiva, conceptos, procedimientos y resultados matemáticos, utilizando el lenguaje oral, escrito, gráfico, multimodal y la terminología apropiados, para dar significado y permanencia a las ideas matemáticas.

Los procesos de comunicación y representación son fundamentales en el aprendizaje de las matemáticas. Conviene distinguirlos porque, si bien están relacionados, no son lo mismo. La cuestión de fondo que habría merecido la pena subrayar es que un objeto matemático va mucho más allá de sus representaciones. Simplificando mucho, podemos decir que las representaciones matemáticas son signos que están en el lugar de objetos, ideas o relaciones matemáticas. Son representaciones matemáticas los símbolos, incluidos –por supuesto– los numéricos, los diagramas, rectas numéricas, tablas, gráficos, disposiciones de manipulables, modelos físicos, fórmulas y ecuaciones. Además de estas representaciones “externas” deberíamos considerar también las que no son visibles o tangibles, “internas”. Estas son las imágenes mentales de objetos geométricos, patrones, formas, etc. La comunicación, por otro lado, es una forma de compartir significados, ideas y, en definitiva, de ganar comprensión de los objetos matemáticos a partir de procesos de interacción, negociación y diálogo.

En la Tabla 8 se recogen los criterios de evaluación que, de nuevo, se desglosan de forma innecesaria por ciclos. Las diferencias de matiz que apreciamos tienden, como en todas las competencias específicas, a utilizar verbos o expresiones que denoten una mayor complejidad en ciclos más altos. Sin embargo, aquí vemos que lo que diferencia el criterio 6.1 es que, en segundo y tercer ciclo, además de reconocer el lenguaje matemático, hay que mostrar y mostrar la comprensión del mensaje. Lo que diferencia unos ciclos de otros no es la capacidad de comprender, es el saber involucrado. Son los saberes que se articulan en las situaciones de aprendizaje los que han de concretar la movilización de las competencias.

Tabla 8. Criterios de evaluación de las competencias del eje de comunicación y representación

3.2.5. Destrezas socioafectivas

Las dos competencias específicas del eje de destrezas socioafectivas son las siguientes:

CE.M7. Desarrollar destrezas personales que ayuden a identificar y gestionar emociones al enfrentarse a retos matemáticos, fomentando la confianza en las propias posibilidades, aceptando el error como parte del proceso de aprendizaje y adaptándose a las situaciones de incertidumbre, para mejorar la perseverancia y disfrutar en el aprendizaje de las matemáticas.

CE.M8. Desarrollar destrezas sociales, reconociendo y respetando las emociones, las experiencias de los demás y el valor de la diversidad y participando activamente en equipos de trabajo heterogéneos con roles asignados, para construir una identidad positiva como estudiante de matemáticas, fomentar el bienestar personal y crear relaciones saludables.

De esta manera, el eje socioafectivo se divide en dos competencias: la CE.M7, que describe las destrezas a alcanzar en el plano personal y emocional; y la CE.M8, dedicada al plano social y a las interacciones. Merece la pena observar que, tanto este eje como el sentido matemático asociado, en los primeros borradores publicados recibía el nombre de “socioemocional”. Pensamos que es un acierto el cambio de nombre por “socioafectivo”, pues las entidades afectivas no quedan restringidas, ni mucho menos, a las emociones.

El hecho de que uno de los ejes competenciales esté dedicado al dominio socioafectivo no hace sino reconocer la importancia que este tiene en el aprendizaje. La relación de lo afectivo y social con lo cognitivo ha sido ampliamente estudiada (véase, p. ej., Beltrán-Pellicer y Godino, 2020; Gómez-Chacón, 2000) y sigue siendo una línea activa de investigación. Es clásica la categorización del dominio afectivo en emociones, actitudes y creencias (McLeod, 1992), tres componentes interrelacionados que se diferencian en términos de intensidad y estabilidad. DeBellis y Goldin (2006) añaden los valores para referirse a compromisos profundos por parte de los individuos que condicionan la toma de decisiones. Otros autores se centran en aspectos como el interés y la motivación (Attard, 2014). Sin embargo, estos últimos pueden explicarse en función de los componentes anteriormente mencionados.

Simplificando mucho la cuestión, es imprescindible visibilizar qué ocurre en el plano emocional, así como diseñar e implementar situaciones de aprendizaje que favorezcan la formación de actitudes y creencias coherentes con las matemáticas que se pretenden construir. Por un lado, si un alumno posee una creencia negativa sobre las matemáticas o sobre su enseñanza, tenderá a mostrar sentimientos adversos hacia las tareas que se planteen, lo que le llevará a conductas de rechazo hacia las matemáticas (Blanco et al., pp. 11-22, 2015). Por otro lado, las diversas situaciones de aprendizaje que va experimentando a lo largo de su vida escolar configuran sistemas de creencias cuyos efectos no se visibilicen hasta que, por ejemplo, se produce un cambio en el contrato didáctico o la cultura de aula. Si el alumnado está acostumbrado a un enfoque expositivo y se pretende seguir un enfoque didáctico abierto a través de la resolución de problemas se produce una ruptura que puede generar cierta resistencia (Brown y Coles, 2013; Sullivan, et al, 2015). Se trata de actuar de forma coherente e insistente, planificando las situaciones de aprendizaje de tal manera que se considere el papel que juegan las creencias y el docente sea consciente del potencial cambio de creencias que tiene lugar (Vila y Callejo, 2004).

La educación, como señalaba Freire (1993), es esencialmente un acto político. En el ámbito particular de las matemáticas y de su enseñanza, autores como Skovsmose y Valero (2001) se han ocupado de estudiar la relación de estas con los valores democráticos. Como era de esperar, la aprobación de la LOMLOE (Jefatura del Estado, 2020) ha suscitado numerosos debates de los que se han hecho eco diferentes medios de comunicación. En el candelero, la eliminación de algunos contenidos “clásicos” en el currículo, como la regla de tres o los números romanos y, sobre todo, el dominio socioafectivo (socioemocional, en los borradores iniciales) y la perspectiva de género (MEFP, 2022). Curiosamente, la cuestión de la regla de tres y los números romanos se puede explicar desde el dominio afectivo. Forman parte del aprendizaje de las matemáticas que hemos vivido muchos de nosotros y, de no estar al tanto de la didáctica, no resulta evidente a ojos del ciudadano su eliminación.

En cuanto a la perspectiva de género, está constatado que no hay diferencia en el desempeño de niñas y niños en matemáticas. Las únicas diferencias que se han identificado son mínimas y restringidas prácticamente al ámbito de la visualización y orientación espacial. Además, estas diferencias pueden explicarse en términos de condicionantes sociales, como la exposición a determinados juegos y juguetes en la infancia. Ahora bien, lo que sí demuestran los estudios de género (Kaiser, et al., 2012; Macho Stadler, et al., 2020) es que hay diferencias significativas de autoconcepto y confianza en uno mismo entre niñas y niños. Ejemplo de ello es la perpetuación de estereotipos de género, como que a los niños se les dan mejor las matemáticas que a las niñas. Esta brecha de género surge ya al comienzo de la Educación Primaria y termina desembocando en una menor participación de la mujer en ámbitos relacionados con las matemáticas y las disciplinas STEM.

La respuesta a todo esto ha de venir desde la concepción de las clases y del enfoque de enseñanza (Boaler y Sengupta-Irving, 2012; Macho Stadler, et al., 2020). Si el profesorado explica y el alumnado se limita a memorizar y a poner en práctica lo dicho, con una evaluación fundamentalmente sumativa, se promueve un ambiente competitivo e individualista. Este proceder ocasiona que las niñas se impliquen menos en su aprendizaje. Por el contrario, un enfoque abierto, colaborativo, donde se discutan las ideas libremente y no se penalice el error, con una evaluación esencialmente formativa, etc. mejora el aprendizaje de todo el alumnado. Otros factores importantes son la elección de los contextos de las situaciones de aprendizaje y dar a conocer las matemáticas como una construcción humana y, en especial, la contribución de la mujer y diversas minorías, históricamente envuelta en dificultades.

Entonces, si la respuesta a la perspectiva de género debería darse desde la creación de un entorno social de aprendizaje, nos resulta llamativo que sea en la CE.M7 donde aparezca mencionada la perspectiva de género de manera explícita. A nuestro modo de ver, sería más adecuada su inclusión en la CE.M8, que es la dedicada al aspecto social del aprendizaje.

Por último, llama también nuestra atención que en el descriptor de la CE.M8 se mencione explícitamente cómo debe formarse ese ambiente de trabajo colaborativo: “participando activamente en equipos de trabajo heterogéneos con roles asignados”. Identificamos aquí técnicas específicas del ámbito del aprendizaje cooperativo y de las funciones ejecutivas. Si el objetivo es crear una cultura de aula colaborativa en donde se haga “visible” el pensamiento, es aventurado –al menos– proponer este tipo de técnicas. Por ejemplo, Liljedahl (2021) llega a la conclusión de que es más adecuado hacer grupos de tres alumnos visiblemente aleatorios. Más aún, al abordar un problema matemático, las tareas no se reparten. Todo el grupo de trabajo participa en todas las fases. Se trata de interactuar.

En la Tabla 9 recogemos los criterios de evaluación de estas competencias. Como en los anteriores, esencialmente son criterios únicos que se matizan innecesariamente a lo largo de los ciclos. De esta forma, el 7.1 implica “reconocer” las emociones en el primer ciclo, mientras que luego se habla de “identificar”. Más confuso resulta que en este criterio, en segundo y tercer ciclo, se señale “pidiendo ayuda solo cuando sea necesario y desarrollando la autoconfianza”; mientras que en primer ciclo no se habla de autoconfianza. Además, “pedir ayuda” ¿implica que los retos son normalmente individuales? En definitiva, pensamos que la evaluación de las competencias del eje socioafectivo, articuladas junto con sus correspondientes saberes, puede llevar a confusión. Si se trata de la misma manera que el resto de competencias y saberes, puede pensarse, incluso, en que hay que calificar de alguna manera este aspecto, cuando lo realmente importante es evaluar qué está pasando en esa dimensión del proceso de enseñanza y aprendizaje para actuar en consecuencia. En realidad, eso es lo que debería hacerse con todos los ejes competenciales, evaluar para orientar la práctica. Sin embargo, con el eje socioafectivo es todavía más claro: ¿son las interacciones adecuadas?, ¿hay algún obstáculo que impida la creación de una cultura de aula coherente con un aprendizaje significativo?, ¿se valora el error como oportunidad de aprendizaje?, etc.

Criterios de evaluación de las competencias del eje de comunicación y representación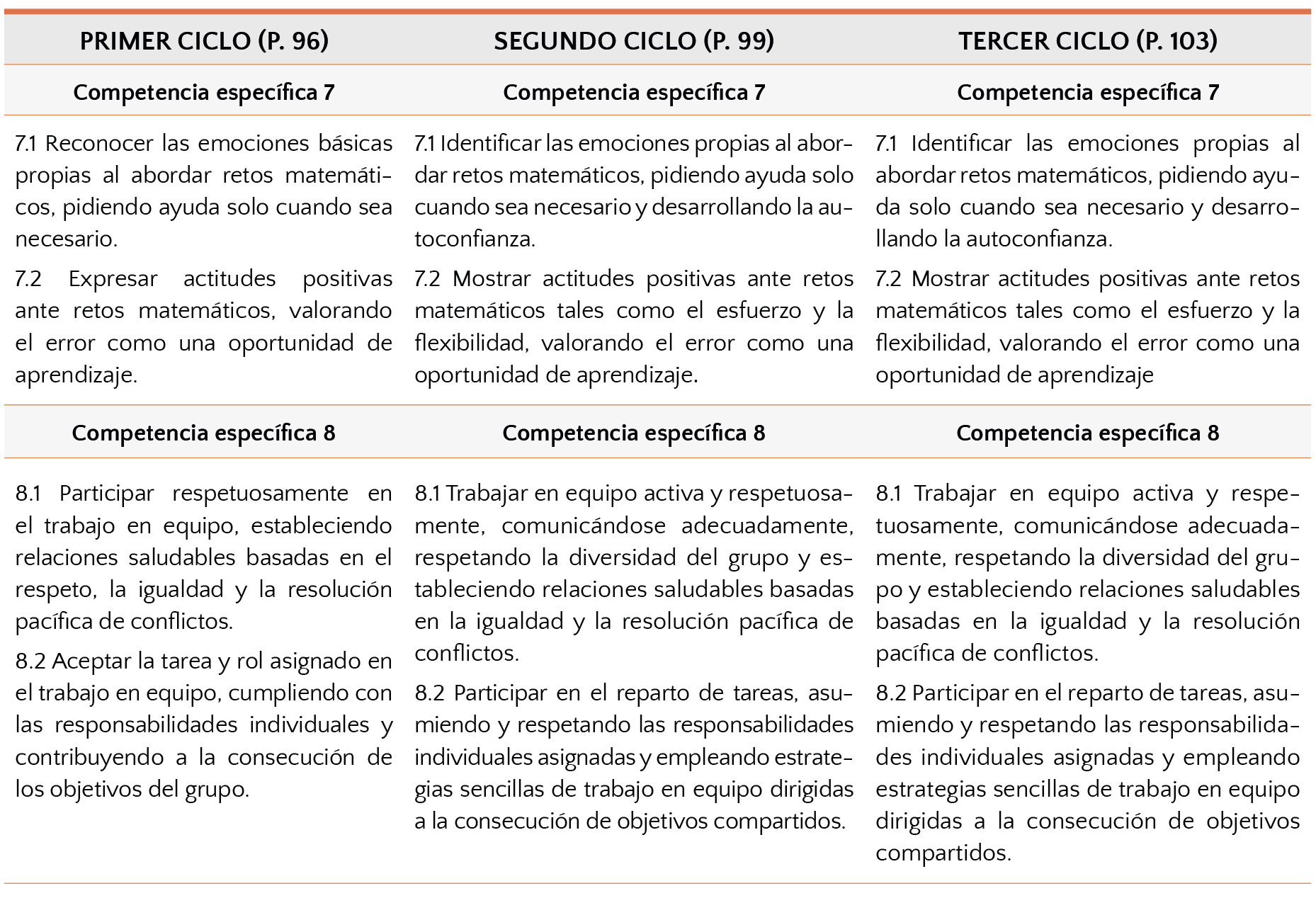

Tabla 9. Criterios de evaluación de las competencias del eje de destrezas socioafectivas

4. REFLEXIONES FINALES

En este artículo se ha revisado la presencia de la competencia matemática en el currículo español vigente de Educación Primaria, el Real Decreto 157/2022, para determinar qué aporta el enfoque competencial a la enseñanza de las matemáticas y, a su vez, ofrecer algunas orientaciones al profesorado interesado en introducir este enfoque de enseñanza en el aula.

Considerando este propósito, se ha puesto de manifiesto que el nuevo currículo supone un paso adelante ya que, en términos generales, propone competencias específicas para promover una enseñanza de las matemáticas basada en pensar y hacer. Alsina (2020) usa el término “práctica productiva” para denominar a estas competencias, asumiendo que en educación matemática una práctica productiva es una acción o destreza educativa útil y provechosa para promover el aprendizaje de las matemáticas con sentido en todos los niveles. En el currículo se consideran cinco prácticas productivas asociadas a las herramientas que nos proporcionan las matemáticas para lograr este propósito: la resolución de problemas, el razonamiento y la prueba, las conexiones, la comunicación y la representación. Estas prácticas productivas o competencias específicas, planteadas inicialmente por el NCTM (2003), son una oportunidad y un desafío para transformar las prácticas centradas en los contenidos, basadas en memorizar definiciones y procedimientos y, en su lugar, desarrollar los distintos saberes para poder usarlos de forma comprensiva y eficaz en diferentes contextos, considerando el dominio socioafectivo.

En este artículo nos hemos centrado fundamentalmente en lo relativo a la competencia matemática, dejando los saberes –agrupados en sus respectivos sentidos– para futuros trabajos. Sin embargo, queremos llamar la atención sobre el hecho de que tres de las ocho competencias específicas tienen una contrapartida explícita con los saberes. De esta forma, la CE.M4 sobre pensamiento computacional se conecta con el bloque de pensamiento computacional dentro del sentido algebraico. Interpretamos que una posible justificación a esta duplicidad puede deberse a esa diferencia entre el proceso de resolución de problemas “general”, propio de las matemáticas, y el proceso de resolución de problemas “computacional”. Las otras dos competencias con esta doble naturaleza son las del eje socioafectivo, a las que se dedica un sentido específico: el sentido socioafectivo. La interpretación en este caso es más complicada. Nos aventuramos a hipotetizar que lo que se pretende es que el profesorado se plantee de forma seria e ineludible el tratamiento del dominio socioafectivo en el aula. No obstante, insistimos en que el dominio socioafectivo incluye también las emociones, actitudes, creencias y valores del profesorado.

Desde un análisis longitudinal o, en otras palabras, desde el punto de vista del horizonte matemático, sorprenden algunas divergencias relevantes en torno a la competencia matemática entre las etapas anterior y posterior a la Educación Primaria. Por un lado, como se ha indicado, en la etapa de Educación Infantil el enfoque competencial es claramente piagetiano, puesto que la competencia matemática se vincula con el desarrollo progresivo de destrezas lógico-matemáticas. Además, se enfatizan exclusivamente las habilidades numéricas, sin explicitar suficientemente las formas de adquisición y uso de los contenidos a través de los procesos de resolución de problemas, razonamiento y prueba, comunicación, conexiones y representación (Alsina, 2022). Por otro lado, gran parte de las conclusiones que hemos extraído de nuestro análisis son extrapolables al currículo de Educación Secundaria Obligatoria (MEFP, 2022b), ya que los ejes competenciales son los mismos. Ahora bien, merece la pena señalar que en el currículo de ESO se describen diez competencias específicas, mientras que, como hemos visto, en el de Educación Primaria hay ocho competencias. Esta discrepancia en el número de competencias se debe a que han sido “desdobladas” las competencias respectivas del eje de conexiones y la del eje de comunicación y representación (Tabla 10).

Tabla 10. Competencias “desdobladas” en el Real Decreto 217/2022, de 29 de marzo, por el que se establece la ordenación y las enseñanzas mínimas de la ESO (MEFP, 2022b)

Consideramos que, en su conjunto, esta falta de coherencia interna acerca de la competencia matemática supone un obstáculo importante para una verdadera transición entre las diversas etapas educativas y, lo que es más importante, dificulta poder interpretar la competencia matemática como una habilidad que se desarrolla de manera paulatina y sistemática a lo largo de toda la escolaridad: ¿por qué, en Educación Infantil, el alumnado se convierte en matemáticamente competente si es capaz de desarrollar habilidades numéricas?, ¿cuál es el papel de las competencias específicas en esta etapa educativa? ¿por qué el alumnado de Educación Primaria se puede considerar matemáticamente competente si es capaz de comunicar y representar en su conjunto, mientras que en Educación Secundaria estas habilidades se deben considerar por separado? o ¿qué fundamentos justifican que en Educación Primaria las conexiones sean una sola competencia, mientras que en Educación Secundaria se desglosan en dos?

Con estos interrogantes finales, más allá de hacer una crítica que no iría a ningún lugar, se pretende poner de manifiesto que desarrollar la competencia matemática implica, en todos los niveles: una gestión de la enseñanza fundamentada en la resolución de problemas, el razonamiento y la prueba, la comunicación, las conexiones y la representación de las ideas matemáticas con base en los conocimientos que el alumnado puede movilizar, considerando en todos los casos el dominio socioafectivo y lo que ello implica. El currículo de Educación Primaria, a pesar de algunas lagunas que se han explicitado en este artículo, contribuye en su conjunto a fortalecer esta visión. Sin embargo, va a ser necesario que en el futuro surjan iniciativas tanto gubernamentales como de las asociaciones de investigadores en educación matemática y de profesores de matemáticas que permitan estrechar los vínculos entre las distintas etapas. Así mismo, es urgente que desde las agendas de investigación en educación matemática sobre la construcción del conocimiento matemático y procesos matemáticos se ofrezcan orientaciones específicas al profesorado para diseñar e implementar prácticas productivas en sus aulas con base en los planteamientos curriculares contemporáneos.

REFERENCIAS

Alsina, Á. (2012). Más allá de los contenidos, los procesos matemáticos en Educación Infantil. Edma 0-6: Educación Matemática en la Infancia, 1(1), 1-14. https://bit.ly/3N3LlzV

Alsina, Á. (2019). Itinerarios didácticos para la enseñanza de las matemáticas (6-12 años). Editorial Graó.

Alsina, Á. (2020). Cinco prácticas productivas para una enseñanza de las matemáticas a través de los procesos. Saber & Educar, 28, 1-13. http://dx.doi.org/10.17346/se.vol0.374

Alsina, Á. (2022). Transformando el currículo español de Educación Infantil: la presencia de la competencia matemática y los procesos matemáticos. NÚMEROS, Revista de Didáctica de las Matemáticas, 111, 33-48. https://bit.ly/3J3SteO

Attard, C. (2014). I don’t like it, I don’t love it, but I do it and I don’t mind: Introducing a framework for engagement with mathematics. Curriculum Perspectives, 34(3), 1-14. https://bit.ly/3L1QXJm

Beltrán-Pellicer, P. y Godino, J. D. (2020). An onto-semiotic approach to the analysis of the affective domain in mathematics education. Cambridge Journal of Education, 50(1), 1-20. https://doi.org/10.1080/0305764X.2019.1623175

Beltrán-Pellicer, P. y Martínez-Juste, S. (2021). Enseñar a través de la resolución de problemas. Suma, 98, 11-21. https://bit.ly/3kZ9rzI

Blanco, L. J., Cárdenas, J. A. y Caballero, A. (2015). La resolución de problemas de matemáticas en la formación de matemáticas inicial de profesores de primaria. Universidad de Extremadura. https://bit.ly/3KXG8YW

Boaler, J. y Sengupta-Irving, T. (2012). Gender Equity and Mathematics Education. En J. Banks (Ed.), Encyclopedia of Diversity in Education. SAGE Publications, Inc.

Bråting, K. (2021). From Symbolic Manipulations to Stepwise Instructions: A Curricular Comparison of Swedish School Algebra Content over the Past 40 Years. Scandinavian Journal of Educational Research, 1-15. https://doi.org/10.1080/00313831.2021.2006301

Brown, L. y Coles, A. (2013). On doing the same problem – first lessons and relentless consistency. En C. Margolinas (Ed.), Task design in mathematics education (Proceedings of the International Commission on Mathematical Instruction Study 22) (pp. 617–626). Oxford, UK.

Casey, K. y Sturgis, C. (2018). Levers and Logic Models: A Framework to Guide Research and Design of High-Quality Competency-Based Education Systems. iNACOL. https://bit.ly/3w0QeE9

CEMAT (2021). Bases para la elaboración de un currículo de Matemáticas en Educación no Universitaria. Comité Español de Matemáticas. https://bit.ly/3ytlGg1

Couso, D. (2017). Per a què estem a STEM? Un intent de definer l’alfabetització STEM per a tothom i amb valors. Ciències, 34, 22-30. https://bit.ly/3L1QzKU

De Bellis, V. A. y Goldin, G. A. (2006). Affect and meta-affect in mathematical problem solving: a representational perspective. Educational Studies in Mathematics, 63, 131-147. https://doi.org/10.1007/s10649-006-9026-4

English, L. D. (2016). STEM education K-12: Perspectives on integration. International Journal of STEM Education, 3(1), 3. https://doi.org/10.1186/s40594-016-0036-1

English, L. D. y Gainsburg, J. (2015), Problem solving in a 21st-century mathematics curriculum. En L. D. English y D. Kirshner (Eds.), Handbook of international research in mathematics education. Third edition (pp. 313-335). Routledge.

European Comission (2004). Europe needs more Scientists. European Commission. https://bit.ly/3sxPiou

Felmer, P., Pehkonen, E. y Kilpatrick, J. (2016). Posing and Solving Mathematical Problems. Springer. https://doi.org/10.1007/978-3-319-28023-3

Fernández-Navas, M. (2015). Internet, organización en red y educ@ción: Estudio de un caso de buenas prácticas en Enseñanza Superior. Tesis doctoral. Universidad de Málaga. https://bit.ly/3sln7ZI

Freire, P. (1993). Política y educación. Editorial Siglo XXI.

Gomez-Chacón, I. M. (2000). Affective influences in the knowledge of mathematics. Educational Studies in Mathematics, 43(2), 149–168.

Ley Orgánica 2/2006, de 3 de mayo, de Educación. https://bit.ly/3wvxhZg

Ley Orgánica 8/2013, de 9 de diciembre, para la mejora de la calidad educativa. https://bit.ly/3Nhyytx

Ley Orgánica 3/2020, de 29 de diciembre, por la que se modifica la Ley Orgánica 2/2006, de 3 de mayo, de Educación. https://bit.ly/39NrMgQ

Kaiser, G., Hoffstall, M. y Orschulik, A.B. (2012). Gender Role Stereotypes in the Perception of Mathematics: An Empirical Study with Secondary Students in Germany. En: H. Forgasz y F. Rivera (Eds.), Towards Equity in Mathematics Education. Advances in Mathematics Education. Springer. https://doi.org/10.1007/978-3-642-27702-3_11

Kilhamn, C. y Bråting, K. (2019). Algebraic thinking in the shadow of programming. Eleventh Congress of the European Society for Research in Mathematics Education (pp. 1-9). Utrecht University.

Liljedahl, P. (2021). Building Thinking Classrooms. Corwin.

Macho Stadler, M., Padrón Fernández, E., Calaza Díaz, L., Casanellas Rius, M., Conde Amboage, M., Lorenzo García, E., & Vázquez Abal, M. E. (2020). Igualdad de género en el ámbito de las Matemáticas. En Libro Blanco de Las Matemáticas (pp. 375–420). Fundación Ramón Areces y RSME. https://bit.ly/3N1NkVa

McLeod, D. B. (1992). Research on affect in mathematics education: A reconceptualization. En D. A. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning (pp. 575-598). Macmillan.

Ministerio de Educación, Cultura y Deporte (MECD, 2014). Real Decreto 126/2014, de 28 de febrero, por el que se establece el currículo básico de la Educación Primaria. https://bit.ly/3yDUhYL

Ministerio de Educación y Formación Profesional (MEFP) (2022a). Real Decreto 157/2022, de 1 de marzo, por el que se establecen la ordenación y las enseñanzas mínimas de la Educación Primaria. MEFP. https://bit.ly/3MWojuA

Ministerio de Educación y Formación Profesional (MEFP) (2022b). Real Decreto 217/2022, de 29 de marzo, por el que se establece la ordenación y las enseñanzas mínimas de la Educación Secundaria Obligatoria. MEFP. https://bit.ly/3MR6Bsu

NCTM (2000). Principles and standards for school mathematics. NCTM.

Niss, M. (2002). Mathematical competencies and the learning of mathematics: the Danish Kom Project. Roskilde University.

OECD (2003). PISA 2003 Assessment Framework: Mathematics, Reading, Science and Problem Solving Knowledge and Skills. OECD. https://bit.ly/3N0TogJ

OECD (2005). La definición y selección de competencias clave. Resumen ejecutivo. OECD. https://bit.ly/3LXVHRE

OECD (2018). PISA 2018 Assessment and Analytical Framework. OECD. https://doi.org/10.1787/b25efab8-en

Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. Basic Books.

Rychen, D.S., Salganik, L.H. y McLaughlin, M.E. (Eds.) (2001). Defining and selecting key competencies. OECD.

Rychen, D.S. y Salganik, L.H. (Eds.) (2003). Key competencies for a successful life and a well-functioning society. OECD.

Salganik, L.H., Rychen, D.S., Moser, U. y Konstant, J. (1999). Projects on competencies in the OECD context: Analysis of theoretical and conceptual foundations. OECD science and problem solving knowledge and skills. OECD.

Shaughnessy, J. M. (2012). STEM: An Advocacy Position, Not a Content Area. Web page. NCTM. https://bit.ly/3P9MUhi

Shaughnessy, J. M. (2013). Mathematics in a STEM Context. Mathematics Teaching in the Middle School, 18(6), 324.

Shute, V. J., Sun, C. y Asbell-Clarke, J. (2017). Demystifying computational thinking. Educational Research Review, 22, 142-158. https://doi.org/10.1016/j.edurev.2017.09.003

Skovsmose, O. y Valero, P. (2001). Breaking political neutrality: The critical engagement of mathematics education with democracy. En B. Atweh, H. Forgasz y B. Nebres (Eds.), Sociocultural research on mathematics education. An international perspective (pp. 37-55). Erlbaum.

Sullivan, P., Knott, L. y Yang, Y. (2015). The Relationships Between Task Design, Anticipated Pedagogies, and Student Learning. En: A. Watson y M. Ohtani, (Eds.), Task Design In Mathematics Education. New ICMI Study Series. Springer. https://doi.org/10.1007/978-3-319-09629-2_3

Vila, A. y Callejo, M. L. (2004). Matemáticas para aprender a pensar: el papel de las creencias en la resolución de problemas. Narcea Ediciones.

Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L. y Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127-147. https://doi.org/10.1007/s10956-015-9581-5

Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33-35.

Yadav, A. y Berthelsen, U. D. (Eds.). (2021). Computational Thinking in Education: A Pedagogical Perspective. Routledge. https://doi.org/10.4324/9781003102991

---