5-2-2020_Practicum_47-64

Resumo

Este estudo, realizado no âmbito da Prática Educativa Supervisionada, Mestrado em Ensino do 1.º CEB e de Matemática e Ciências Naturais no 2º CEB, foi desenvolvido numa turma de 4º ano e teve como objetivo promover melhoria na resolução de problemas envolvendo a operação divisão. Desenharam-se três objetivos específicos: analisar a influência do método de Polya na resolução de problemas; perceber a abordagem da gamificação na motivação e envolvimento dos alunos; compreender o efeito de recursos tecnológicos digitais no processo de aprendizagem. Seguindo metodologia de investigação-ação e abordagem mista, utilizaram-se instrumentos de recolha de dados: observação participante, diário do projeto, aplicação de um pré-teste e pós-teste. Verificou-se que o método de Polya ajudou a melhor compreender e organizar o problema, fomentando autonomia na resolução do mesmo; a gamificação estimulou o entusiasmo e o desejo dos estudantes atingirem os seus objetivos; os recursos digitais facilitaram a articulação curricular e capacidades de colaboração.

Abstract

This study done in the Master of Mathematics of the 1st Educative cycle and Natural Science of the 2nd Educative Cycle, in the discipline of Supervision in Educative Practice, was developed with 4th grade students with the aim of improve problem solving with the division operation. Three specific objectives were designed: analyze the influence of Polya’s method on problem solving; understand the gamification approach in student motivation and involvement; understand the effect of digital technological resources on the learning process. Data collection instruments were used, following action research methodology and mixed approach: participant observation, project diary, application of a test before (pretest) and after (posttest) the training situations. We verify that the Polya’s method helped to better understand and organize the problem, promoting autonomy in solving it; the gamification has stimulated students’ enthusiasm and desire to achieve their goals; digital resources facilitated curriculum articulation and collaboration capabilities.

Palavras-chave

Resolução de problemas, Método de Polya, Gamificação, Tecnología da Informação e da Comunicação.

Keywords:

Problem solving, Polya’s Method, Gamification, Information and Communication Technologies.

1. Introdução

É do conhecimento geral a importância que a Matemática assume em várias áreas do conhecimento e, por essa razão, é cada vez mais importante que esta seja compreendida por todos aqueles que a estudam. Desde há muito tempo, que existe um descontentamento por parte dos alunos e por parte dos professores relativamente à Matemática. Tal situação é identificada pelos órgãos competentes, responsáveis por avaliações nacionais e internacionais, como por exemplo, o Programa Internacional de Avaliação de Estudantes (PISA) (Marôco, Gonçalves, Lourenço & Mendes, 2016).

De facto, ao longo dos anos, tem-se vindo a comprovar que a Matemática é, sem dúvida, a ciência que melhor permite analisar o trabalho da mente e desenvolver um raciocínio aplicável ao estudo de qualquer temática. Contudo, talvez porque foram criados hábitos mentais difíceis de serem quebrados, muitas são as dificuldades que os alunos encontram no seu estudo. Ora, é possível que esta situação ocorra uma vez que provavelmente não existe uma explicitação concreta da relação entre os conteúdos e a realidade das crianças. Saliente-se que ensinar Matemática sem explicitar a origem e as finalidades dos conceitos é contribuir para o insucesso escolar (Ponte, 2005). Neste sentido, sendo um dos objetivos preponderantes da educação dar oportunidade de construir conhecimentos e desenvolver competências, capacidades e atitudes, emerge a necessidade da implementação de uma moderna educação matemática que vise relacionar o programa e métodos de ensino para que o professor reflita sobre o que está a ensinar, o modo como o faz e a pertinência do que ensina (Mascarenhas, Maia & Martínez, 2017). Na verdade, a resolução de problemas é uma capacidade que pode ser trabalhada de forma articulada com os diferentes conteúdos programáticos, embora tal não esteja muito evidenciado no atual programa do ensino básico. No entanto, de acordo com o National Council of Teachers of Mathematics (NCTM), a resolução de problemas deve ser o centro do currículo de matemática (NCTM, 1980), visto que os alunos ao desenvolver um trabalho mental, um trabalho de exploração pelos seus próprios meios, poderão desenvolver um processo de ensino e aprendizagem com mais significado e mais sentido nas suas vidas (Polya, 2003). Neste sentido, a resolução de problemas assume um papel basilar na formação do aluno, uma vez que é uma ferramenta fundamental na sua aprendizagem. Além disso, promove o desenvolvimento de competências inerentes à tomada de decisões, construindo uma melhor qualidade de vida (United Nations Educational, Scientific and Cultural Organization [UNESCO]- Windham, 1990).

No entanto, são vários os estudos nacionais e internacionais que apontam para as dificuldades dos alunos portugueses na resolução de problemas, nomeadamente, problemas que envolvam a operação aritmética divisão (Marôco, Gonçalves, Lourenço, & Mendes 2016); Monteiro, 2018; Sampaio, 2018). Tal foi possível verificar pela investigadora, aquando da realização da sua prática de ensino supervisionada. Durante a sua ação, verificou-se que os alunos, quer ao nível do ensino do 1.º Ciclo do Ensino Básico (CEB) quer do 2.º CEB, evidenciaram muitas dificuldades na compreensão da operação divisão, embora fossem capazes de aplicar, de forma mecânica, o algoritmo convencional de divisão inteira. No entanto, quando lhes era apresentado um problema, envolvendo esta operação, os mesmos revelaram muitas dificuldades.

Assim, considerou-se fulcral investigar esta temática, com o intuito de se contribuir para a melhoria da aprendizagem dos estudantes, no 1.º CEB, no sentido de se proporcionar a compreensão da operação divisão inteira, bem como, permitir que os alunos sejam capazes de resolver problemas que envolvam esta operação. Para tal, pretendeu-se com esta investigação, desenvolver e aplicar um conjunto de tarefas, elaboradas com auxílio das novas tecnologias, aliando as propriedades e características da gamificação e, paralelamente, abordar o método de Polya para a resolução de problemas.

2. A Resolução de Problemas e o Método de Polya

Nos dias de hoje, cada vez mais se enfatiza a Resolução de Problemas (RP) no ensino da matemática, uma vez que acompanha a vida de qualquer pessoa em várias atividades e sob diversas situações. Para além da resolução de problemas matemáticos estar presente, em todos os anos, no currículo do ensino básico, esta atividade é essencial dado que possibilita que os alunos verifiquem as potencialidades da Matemática no quotidiano de cada cidadão (Vale & Pimentel, 2004; Monteiro, 2018). Assim, torna-se determinante aprender e compreender a Matemática, uma vez “que contribui para a formação de indivíduos responsáveis, autónomos, interventivos e criativos” (Mascarenhas, Maia, & Martínez, 2017, p. 46).

A resolução de problemas, uma das sete capacidades elencadas pelo PISA (Marôco, Gonçalves, Lourenço, & Mendes 2016) nos processos matemáticos, “é uma atividade estruturada que desenvolve diversas capacidades cognitivas” (Monteiro, 2018, p. 107), uma vez que articula “a organização da informação, o conhecimento de estratégias, as diferentes formas de representação, a tradução de linguagens, a aplicação de vários conhecimentos, a tomada de decisões, a interpretação da solução” (Vale & Pimentel, 2004, p.11).

Nesta ordem de ideias, Boavida et al (2008) referem que a resolução de problemas:

proporciona o recurso a diferentes representações e incentiva a comunicação; fomenta o raciocínio e a justificação; permite estabelecer conexões entre vários temas matemáticos e entre a matemática e outras áreas curriculares; apresenta a Matemática como uma disciplina útil na vida quotidiana (Boavida et al., 2008, p. 14).

Na verdade, já há muito tempo que a RP está presente nos currículos de ensino, no entanto é necessário que lhe seja atribuído outro significado, para além do simples papel da consolidação de problemas: o problema poderá ser o ponto de partida para a aprendizagem, e não apenas se limitar ao termino de um assunto ou conteúdo. Neste sentido, emerge a necessidade de se encontrar um caminho, que permita determinar a solução, construindo um conjunto de ações pensadas que formule uma solução denominado por Resolução de Problemas (Vale & Pimentel, 2004). Assim, é necessário que os alunos tenham a oportunidade de momentos em que possam explorar, partilhar ideias, refletir sobre as soluções ou caminhos a seguir, para que consigam analisar o resultado obtido.

Várias são as definições existentes para o conceito de problema. Segundo Polya (1980) estamos perante um problema quando se pretende descobrir um caminho que auxilia a contornar um obstáculo, mas que não se acessa de imediato. Lesh e Zawojewki (2007, citado por Vale, Pimentel, & Barbosa, 2015) afirmam que “uma tarefa [se] transforma (…) num problema quando o resolvedor (…) tem de desenvolver um modo mais produtivo de pensar acerca da situação dada” (p. 44), tendo que analisar o enunciado, desenvolvendo métodos que proporcionam a “base da modelação matemática” (Idem, p.44).

No que diz respeito à resolução de problemas, é de referir que não existe um único método para resolver problemas, nem nenhuma fórmula para ensinar a resolver problemas (Vale & Pimentel, 2004; Monteiro, 2018), mas um dos métodos mais conhecidos e valorizados no ensino da Matemática, é o método apresentado por George Polya (1973) que estabeleceu quatro etapas fulcrais para a RP: compreensão do problema, estabelecimento de um plano, execução do plano e verificação. Na primeira etapa, compreensão do problema, pretende-se que o aluno leia o enunciado, identifique os dados e a incógnita: “Qual é a incógnita? Quais são os dados? Qual é a condicionante?” (Polya, 1977, p. 8). Na segunda etapa, estabelecimento de um plano, o aluno, através dos seus conhecimentos prévios, identifica as relações entre problemas que já tenha resolvido, a fim de delinear a estratégia mais adequada: “Já o viu antes?”, “É possível utilizá-lo?”, “É possível reformular o problema?”, “Utilizou todos os dados? Utilizou toda a condicionante?” (Polya, 1977, p. 10). Na terceira etapa, execução do plano, o aluno resolve o problema verificando se a estratégia escolhida resultou ou não, e caso não tenha resultado, tem de voltar à etapa anterior: “É possível verificar claramente que o passo está correto?” (Polya, 1977, p. 13). Na quarta e última etapa, verificação, verifica-se se a solução obtida responde à questão do problema, estando de acordo com os dados identificados: “É possível verificar o resultado? É possível verificar o argumento?” (Polya, 1977, p. 14).

Posto isto, ao longo dos anos, o modelo proposto por Polya para a RP tem servido como referência para grande parte dos estudos realizados nesta área, valorizando-se, deste modo, a sua obra como um marco referente a esta temática. No estudo realizado por Monteiro (2018), a autora refere que o conhecimento do método de Polya permitiu aos alunos maior motivação para o ensino da Matemática, contribuindo para terem sucesso na resolução de problemas.

3. Gamificação na Educação

As tecnologias emergentes são promotoras de mudanças, pelo que quando integradas na educação também transformam os modos de ensinar e de aprender, de comunicar, de relacionar e até mesmo a conceção de significados. A gamificação é um exemplo relevante no Século XXI, pois os games fazem parte da vida desta nova geração. Aproveitando a predisposição das crianças e jovens para o jogo, o conceito associa-se a ambientes lúdicos com o propósito de as cativar e envolver no processo de aprendizagem. Assume-se como uma abordagem que estimula a recompensa e os feedbacks num processo colaborativo motivando os alunos. Por esta razão, diz-se que ela pode atenuar um problema social da escola, como o da desmotivação dos seus alunos. Assim, sendo um imput à motivação dos alunos (Ruben, 1999), a gamificação transfere a mecânica do jogo a ambientes educativos com o propósito de estimular aprendizagens ativas que melhorem resultados, mas também que desenvolvam capacidades e atitudes (Amador, 2018). Este processo facilita a inclusão de todos os alunos na aprendizagem.

Zichermann e Linder (2010) associam a gamificação a um processo de Game Thinking no qual os alunos aprendem através de um jogo sem se aperceberem que estão a jogar, ou até mesmo o contrário, sabem que estão a jogar um jogo, mas não se apercebem que estão a aprender e a adquirir conhecimentos e competências do perfil do aluno. Também Zichermann e Cunningham (2011) reforçam a ideia da gamificação detentora de regras e de desafios e, ainda, de outros elementos essenciais que transformam as atividades educativas num ambiente lúdico e dinâmico e fomentam um ambiente de conquista de objetivos. A exemplo temos a Gamification Framework, conhecida por Octalysis (Chou, 2016), que apresenta oito eixos (Core Drives) como num processo de atingir metas. Inicia num desafio que envolve e motiva a crianças num ambiente criativo e potenciador de ação, de sentimento de posse e necessidade de interação, comunicação. A recompensa inquieta as crianças numa descoberta gradual das atividades para atingir os objetivos da aula. Assim, em situação de jogo, relevam-se os elementos visuais que atraem as crianças estimulando a atenção e grandes momentos de concentração (Deterding, 2011). Relevam-se, ainda, os sistemas de recompensa e de feedback, objetivos e regras claras, a interatividade, a diversão, a cooperação e a competitividade (Fardo, 2013); a possibilidade de progressão de forma gradual, através de níveis e possibilidade de obter pontos que conduzem à vitória, o investimento e a teoria da informação em cascata, fatores importantes no alcance de objetivos propostos (Souza, Lopes & Silva, 2013).

No que diz respeito ao investimento por parte do aluno, é relevante que este tome consciência da importância do compromisso e do processo colaborativo para atingir uma conquista, sendo que o professor deve facilitar o processo estimulando práticas colaborativas. Note-se que o jogo ajuda a compreensão de situações complexas reais e orienta os jogadores na ação, na comunicação, na tomada de decisão e na conquista de um objetivo comum, pois os jogadores sabem claramente os objetivos do jogo e o que precisam de fazer para atingir a meta. Além disso, destacam-se as contribuições dos alunos e a sua reputação no grupo (Richter, Raban, & Rafaeli, 2015) e a promoção de experiências positivas que fomentam o esforço, a fidelização e a cooperação na aprendizagem (Amador, 2018). Neste processo, os alunos desenvolvem diferentes competências entre elas a de autonomia e responsabilidade, o saber viver juntos e capacidades de literacia digital (Kapp, 2012). No que diz respeito às implementações, estas incluem propriedade (pontos, medalhas, crachás), realizações (uma representação de realização), status (classificação ou nível), colaboração (desafios que podem ser resolvidos trabalhando juntos) (Vassileva, 2012). Estes elementos convergem no sentido de tornar a aprendizagem significativa, mais profunda, eficaz e duradora (Souza, Lopes & Silva, 2013). Por outro lado, segundo o autor, os alunos valorizam mais o trabalho do professor e podem mesmo valorizar as suas aprendizagens, embora às vezes de uma forma inconsciente (idem). O estudo de Andrade, Quadros-Flores e Pinto (2019) mostra que a gamificação tem repercussões na criança ao nível cognitivo, emocional e social, sendo promotora de capacidades, atitudes e valores.

4. Questões e objetivos de investigação

A partir da problemática mencionada anteriormente, foram definidas três questões orientadoras:

Questão 1: De que forma a gamificação interfere na atitude dos alunos face à matemática?

Questão 2: Que contributo poderá ter para os alunos o conhecimento do método de Polya na Resolução de Problemas de um ou de dois ou mais passos envolvendo a operação divisão?

Questão 3: De que forma a utilização de recursos digitais pode contribuir para melhorar a construção de enunciados?

Neste sentido, foram definidos os seguintes objetivos de investigação:

Objetivo geral: melhorar o desempenho dos alunos na resolução de problemas que envolvam a operação divisão.

Objetivo 1: Compreender a forma como uma estratégia lúdica (gamificação) pode envolver o aluno na construção de conhecimento matemático.

Objetivo 2: Analisar a influência da aprendizagem do método Polya nos alunos na resolução de problemas envolvendo a operação divisão.

Objetivo 3: Averiguar se a utilização das novas tecnologias ajuda os alunos na compreensão dos enunciados de problemas.

5. Metodologia

A escolha da metodologia de investigação pressupõe a seleção de estratégias, baseando-se na natureza do problema em estudo e nos objetivos que se pretendem atingir, e é através destes que se selecionam as ferramentas de recolha de dados (Sousa & Baptista, 2011). Nesta linha de pensamento, o presente estudo segue metodologia de investigação-ação que, através da observação de certos fenómenos num contexto específico, pretende “produzir conhecimento, modificar a realidade e transformar os actores” (Simões, 1990, citado por Almeida & Freire, 2000, p.30). Esta metodologia articula a ação com a investigação, baseando-se num ciclo em que o agir leva ao refletir, de forma a melhorar aprática educativa (Coutinho et al., 2009). Assim, este estudo revela o processo de crescimento pelas etapas do ciclo de investigação-ação: observar, planear, agir e refletir. Para a recolha de dados recorreu-se a uma metodologia predominantemente qualitativa, de modo a se poder compreender a ação dos que estão a ser investigados, de uma forma exploratória, descritiva e indutiva (Carmo & Ferreira, 2008).

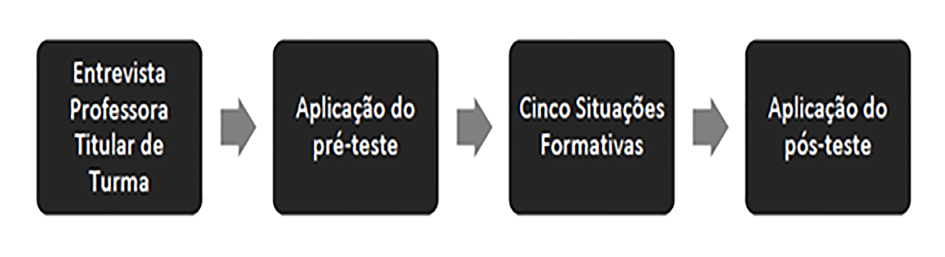Figura 1, Síntese das fases de recolha de dados.

Fonte: elaboração própria

Para além disso, atendendo à natureza do problema e aos instrumentos de recolha de dados, que a seguir se caracterizam, esta investigação segue uma metodologia mista mas predominantemente qualitativa, de natureza descritiva e interpretativa. A opção do paradigma interpretativo justifica-se pela “natureza aberta, globalizante e compreensiva” das questões orientadoras do presente trabalho de investigação (Martinho, 2011, p. 105).

Importa ainda referir que é um estudo de caso e segundo Latorre et al. (2003, citado por Meirinhos & Osório, 2010), esta estratégia visa percorrer uma “lógica que guia as sucessivas etapas de recolha, análise e interpretação de informação dos métodos qualitativos, com a particularidade de que o propósito da própria investigação é o estudo intensivo de um ou poucos casos” (p.52). Assim, este estudo foi aplicado numa turma do 4.º ano do 1.º CEB. A turma era construída por 20 alunos, dos quais 10 eram do sexo feminino e 10 do sexo masculino. Os alunos têm idades compreendidas entre os 8 e 10 anos, sendo que um deles tem necessidades educativas especiais, pelo que necessitou de um acompanhamento mais próximo e cuidado, por parte da mestranda, ao longo do desenvolvimento do projeto. O contacto entre a turma-alvo e a mestranda foi estabelecido três dias por semana, num bloco de 60 minutos, durante um mês.

5.1. Instrumentos utilizados para recolha de dados

Para a recolha de dados recorreu-se à aplicação de um teste, em dois momentos diferentes: antes das situações formativas, pré-teste, e após as situações formativas, o pós-teste. Para além deste instrumento de recolha de dados, também se recorreu à observação participante, conseguindo-se recolher informações adicionais à investigação, pelo registo de situações fulcrais para a temática em estudo. Além do mais, através das situações formativas, recolheu-se dados de forma a tentar perceber a evolução da amostra na resolução de problemas que envolvam a operação aritmética divisão, na formulação de problemas, recorrendo a desafios, jogos online e às tecnologias, num trabalho colaborativo entre os alunos. A análise de documentos foi outra das técnicas estipuladas, tendo analisando documentos pessoais. Isto é, documentos criados pelo próprio investigador para registo próprio ou por outras pessoas (Latorre, 2005). Neste sentido, a investigadora criou o diário do projeto, distribuído a cada aluno, para que os alunos pudessem cola os desafios recebidos, assim como todos os documentos entregues pela investigadora. Mais ainda, a investigadora consultou alguns documentos da amostra, como a ficha de perfil de turma. Outro dos instrumentos de recolha de dados utilizados, foi a entrevista focalizada à professora titular de turma, com o objetivo de recolher informação basilar acerca da caracterização do contexto e de se perceber as maiores dificuldades da turma na temática em estudo. Saliente-se que o cruzamento destas técnicas e instrumentos supramencionados, permitiram um cruzamento de diferentes olhares de modo a ampliar a perspetiva do investigador (Bogdan & Biklen, 1994).

É importante referir que foi criada uma história “O que brilha lá no alto?” que completou e orientou o projeto, tornando-se o elo de ligação entre todas as situações formativas. Devido a alguns conflitos, entre os pares, observados na turma, na primeira semana de contacto, a investigadora optou por criar uma história que levasse os alunos a refletirem sobre o comportamento manifestado, postura e relações. Neste sentido, a história focou a importância da amizade verdadeira e no quanto esta pode melhorar a vida de todos, envolvendo-a sempre que possível nas situações formativas. Note-se que se estabeleceram os grupos de trabalho para o projeto (5 grupos de 4 elementos), comparando significativamente o trabalho de cooperação a realizar com a história criada. Da mesma forma que as personagens só chegavam ao local pretendido com a ajuda dos amigos, também neste projeto, os alunos só consegue, alcançar o pretendido com o apoio de todo o grupo de trabalho, destacando-se, deste modo, um foco desta investigação, promover o trabalho colaborativo entre os alunos.

O projeto envolveu a “gamificação” que, de forma transversal, acompanhou o desenvolvimento das unidades de aprendizagem. Assim, cada Situação Formativa (SF) envolvia um conjunto de estratégias que permitia a compreensão do conteúdo curricular e o desenvolvimento de competências. A SF correspondia a um nível a ser ultrapassado e, por sua vez, o acumular de pontos, posteriormente reconhecidos em prémios. Reforçou-se aqui a progressão para recompensar os grupos que completavam a unidade. Contudo, para os que não conseguiam passar um determinado nível deu-se a oportunidade de entrarem num novo ambiente de aprendizagem que fomentava novos desafios de resolução de problemas permitindo o alcance de nível e dos referidos pontos, ou seja, deu-se oportunidade aos alunos de atingirem sempre os níveis, na base de tentativa e erro, e nunca a hipótese de desistência. É de salientar que as recompensas foram pensadas tendo em atenção os interesses dos alunos. Mais ainda, foi criado um cenário na sala de aula que permitia registar, de forma visível, as posições dos grupos no “jogo”, as suas dificuldades, as aprendizagens adquiridas e os pontos obtidos em cada SF.

Note-se que este estudo teve como objetivo melhorar o processo de aprendizagem da resolução de problemas envolvendo a operação da divisão, estabeleceram-se três objetivos específicos: (I) analisar a influência do método Polya na resolução de problemas; (II) perceber a abordagem da gamificação na motivação e envolvimento dos alunos, servindo de alavanca impulsionadora do aumento do esforço para atingir metas (III) compreender o efeito de recursos tecnológicos digitais no processo de aprendizagem.

5.2. Caracterização do estudo

O projeto de investigação aqui presente ocorreu entre outubro e novembro de 2018. Note-se que esta investigação visou ensinar os alunos a aprender a aprender a ultrapassar as dificuldades na resolução de problemas de dois ou mais passos que envolvam a operação divisão, tendo como aliada as novas tecnologias e a gamificação. Posto isto, através da Figura 1, pode analisar-se as quatro fases constituintes do projeto, que foram determinadas pelo problema e questões de investigação e dos objetivos delineados para o estudo.

Tal como se observa na figura mencionada, a primeira fase da recolha de dados baseou-se na entrevista à Professora titular de turma, sendo esta crucial para o conhecimento das características da turma (os seus gostos, necessidades, comportamento, postura, etc.) onde se realizou o estudo, assim como para o diagnóstico das dificuldades dos alunos na temática em questão. Neste sentido, a entrevista foi organizada em 41 questões que constituíam nove domínios: habilitações académicas e percurso profissional; rotina profissional e estratégias/método de ensino – materiais e recursos; estratégias/métodos de ensino – caracterização do espaço; estratégias/método de ensino – tempo; estratégias/método de ensino – grupo de crianças; atividades e projetos; relação escola – família/comunidade; relação docente – aluno e, por ultimo, conteúdo matemático: divisão.

Posteriormente, foi aplicado, aos alunos em estudo, um teste escrito de avaliação de conhecimentos. Este documento foi denominado por pré-teste e pós-teste, uma vez que se aplicou o mesmo teste em dois momentos diferentes: no início do projeto e no fim do mesmo. Este documento continha quatro itens, sendo o primeiro criado pela mestranda, de aplicação direta de algoritmos da divisão exata e os restantes de resolução de problemas, de um ou mais passos, que envolveram a operação aritmética divisão, retirados e adaptados de provas de aferição do 1ºCEB. Este documento foi o principal instrumento de recolha de dados, embora existam outros elementos a serem analisados como o diário do projeto de cada aluno e os registos da mestranda em cada situação formativa. O objetivo da aplicação do teste em dois momentos diferentes, visou averiguar, se após as situações formativas orientadas pela mestranda, houve uma evolução no desempenho dos alunos, e consequentemente nos seus conhecimentos.

Estratégias	Resultados
Construção de avatares por parte dos alunos	No processo colaborativo verificou-se - que havia crianças que assumiam o papel de líder; - que todas tiveram oportunidade de participar; - que as discussões permitiram às crianças tomar decisões; - que o grupo conseguiu realizar as tarefas e atingir objetivos mais elevados. No processo de construção do enunciado verificou-se - que inicialmente tiveram mais dificuldades, mas que o trabalho em equipa ajudou a ultrapassar barreiras, nomeadamente de escrita, de formulação de problemas, técnicos. - que aumentou o esforço do grupo em querer realizar a tarefa. - que o facto de o avatar apresentar os seus enunciados motivou os alunos que tinham orgulho no avatar que era seu.
Apresentação oral dos enunciados	Verificou-se - entusiasmo pelos grupos ao apresentarem os seus avatares e organização na apresentação. - Quanto à discussão, que os alunos ainda têm dificuldades em aceitar opiniões divergentes das suas, no entanto conseguiam compreender os diferentes pontos de vista, mesmo não concordando.
Realização do livro on-line	Verificou-se - que o facto de se optar pela construção de um livro on-line com os seus trabalhos entusiasmou os alunos pela sua aparência (bonito, colorido…) e porque se reviam no trabalho final. - que o facto deste livro ser criado de uma forma mais motivadora, no computador e com recurso a várias ferramentas, fez com que os alunos estivessem realmente empenhados e motivados para o que foi pedido. - que a possibilidade de o partilhar com a família e com os amigos da escola, influenciou positivamente o seu entusiasmo. Como o livro está gravado online, havia um link associado para quem quisesse ver o trabalho da turma.
A utilização de recursos tecnológicos digitais	Verificou-se - que a utilização do computador e de aplicações interativas on-line permitiu que só alunos desenvolvessem conteúdos matemáticos e de português de uma forma mais motivadora e entusiasmante. - que ajudou na consciencialização da linguagem matemática.

Tabela 1, Relação estratégia/ efeito com recursos tecnológicos digitais

Fonte: elaboração própria

6. Apresentação e discussão de resultados

Analisando os dados obtidos nos dois momentos de avaliação, foi possível apurar uma melhoria nas aprendizagens médias globais dos alunos, tendo no pré-teste recolhido uma percentagem média total de 65,2% e no pós-teste 73,54%.

Em relação às situações formativas, é possível afirmar que ao longo do percurso delineado, os alunos tornaram-se cada vez mais entusiasmados com o projeto, notando-se claramente uma maior motivação, uma vez que em cada SF vários foram os comentários que transmitiam isso, nomeadamente “Professora hoje é o projeto outra vez? Que fixe!” “Podemos jogar este jogo todos os dias?”. Além dos mais, ao longo de todas as situações formativas, foi possível observar uma evolução nas respostas dos alunos. Em certos desafios iniciais, os alunos esqueciam-se de algumas etapas, porque não estavam habituados ao método de Polya, no entanto ao longo do projeto, foram reconhecendo as etapas de Polya como uma mais-valia, e que os ajudavam na compreensão e resolução do problema. Aliás, tal é possível verificar-se se se atentar nas respostas dadas no pré-teste e pós-teste.

O cenário criado na sala de aula, revelou-se essencial para o reconhecimento e dificuldades da turma. Os próprios alunos iam frequentemente analisar o cenário, identificando as dificuldades uns dos outros e para ver quem estava quase a passar de nível ou não. Para a investigadora, esse espaço foi basilar, porque no fim de cada sessão de trabalho, os cartões utilizados para colar os pontos dos grupos, e para saber quem passou ou não de nível, eram os cartões dos registos da investigadora. Sendo desta forma, de rápida leitura e acesso: tanto pela cor (verde se alcançaram os pontos pretendidos, laranja caso não), tanto pelo que lá estava registado (as dificuldades e os pontos a melhorar). Numa das situações formativas, os grupos tiveram de criar um texto no qual explicassem as vantagens do método de Polya. E para além de se ter criado um momento de partilha entre todos, foi possível aferir as vantagens do método referido na perspetiva dos alunos. Todos os grupos consideraram que “o método de Polya ajuda a resolver os problemas mais difíceis” e “que a partir de agora vão usá-lo na resolução de problemas” (frases escritas pelos alunos). Mais ainda, houve um grupo que aferiu “com este método nós aprendemos que antes de resolvermos o problema, temos de compreendê-lo”.

Com a criação de um livro online, através do storyjumper, cada grupo criou uma página, criando-se um livro que foi apresentado à turma. Através da análise desse livro, conseguiu-se aferir as aprendizagens dos alunos, o que mais gostaram e as dificuldades ultrapassadas. Note-se que apesar de a investigadora ter orientado o trabalho dos alunos com algumas questões e pontos orientadores, foi decisão dos alunos o que iriam escrever, podendo acrescentar outros pontos. Repare-se que aquilo que todos os grupos mais gostaram foi de “ter aulas diferentes” e de “jogar um jogo” enquanto aprendiam matemática. Além disso, todos consideraram também que “aprenderam a resolver problemas e a perceber os enunciados”. Em três grupos, ou seja, 16 alunos, consideraram importante a história e o trabalho de grupo, como construção de aprendizagens essenciais a vários níveis.

De uma forma geral, observando os registos obtidos por observação direta e análise documental ao longo de todos os momentos do projeto, a investigadora considera que os alunos conseguiram reconhecer o método de Polya como uma mais-valia na resolução de problemas que envolvam a operação divisão, e o mais importante, conseguiram compreendê-lo e utilizá-lo.

6.1. Caracterização do estudo

Os resultados revelam que o método de Polya ajudou a melhor compreender e organizar o problema fomentando autonomia na resolução do problema. Analisando as cotações obtidas no pré-teste e no pós-teste, foi possível verificar que existiu uma melhoria na média global dos testes de 8,34% (passou-se de 65,2% para 73,54%). Foi notório que com o auxílio do método de Polya, os alunos melhoraram o seu desempenho, pelo que se pode concluir que as situações formativas tiveram efeito positivo na aprendizagem dos alunos em estudo, em particular, pode afirmar-se que o método de Polya contribuiu para o aumento da percentagem de sucesso na resolução de problemas envolvendo a operação divisão. Além do mais, analisando o modo como os alunos resolveram os problemas nos dois momentos de avaliação, pode constatar-se uma aprendizagem das etapas do método de Polya e que estas os ajudaram na estruturação do seu pensamento e na organização da resolução. Assim, é possível afirmar que as situações formativas criadas com a amostra, originaram resultados na aprendizagem dos alunos, ajudando-os a organizar os dados e as suas respostas.

6.2. Abordagem da gamificação na motivação

e envolvimento dos alunos

A gamificação é sem dúvida algo inovador e gratificante sob várias perspetivas. A observação participante permitiu compreender que o facto de se aliar conteúdos matemáticos a propriedades e características de um jogo facilitou a tomada de consciência do desafio da aula. Através dos diálogos criados, foi possível apurar que os alunos se sentiam mais entusiasmados por terem metas a atingir, como o alcance dos pontos pretendidos. Ao receberem pontos por cada desafio superado, fez com que os alunos trabalhassem para obterem o máximo de pontos possível. Além disso, as tarefas extra eram bem aceites pelos alunos, uma vez que estes viam nelas oportunidades de ganhar mais pontos e recuperar os pontos perdidos ao longo das situações formativas.

É possível afirmar que as propriedades da gamificação tiveram um efeito motivador e aliciante nos alunos, o que leva a crer que estes possuem uma motivação intrínseca que facilita este tipo de atividades, pois vai ao encontro dos seus interesses. Constatou-se que até os alunos mais reservados, e aparentemente mais desmotivados, no fim do projeto estavam com uma postura bem mais participativa e cooperativa. De relevar que a gamificação exigiu um trabalho colaborativo por parte dos alunos que se tornou essencial em todo o processo. Acresce que este tipo de atividades quebrou a rotina das práticas educativas fomentadas até então e acrescentou valor à aula, pois foi bastante enriquecedor a dinâmica das equipes, a capacidade de partilha de ideias, de decisão, liderança e respeito pelos outros. Mais ainda, notou-se que as relações entre os pares foram fortalecidas, indo ao encontro de uma das intencionalidades do projeto: valorização da amizade e das relações (explanada na história criada para acompanhar todo o projeto).

6.3. O efeito de recursos tecnológicos digitais

no processo de aprendizagem

Partiu-se do princípio que as tecnologias podem favorecer a compreensão da Formulação de Problemas (FP) se estes forem construídos pelas crianças. Esta potencialidade da criança no processo de aprendizagem (dinâmica da gamificação) assumindo-se como jogadora e potenciadora da construção dos seus saberes na interação com o grupo, onde todos são responsáveis pelo seu comportamento e resultados da aprendizagem, motiva-a para alcançar objetivos. Neste sentido, deu-se oportunidade aos grupos de definirem estratégias utilizando uma aplicação on-line e interativa que permite a construção de avatares. Neste processo, era esperado que os alunos construíssem enunciados de problemas baseados nas soluções apresentadas, para melhor compreenderem a estrutura da formulação de problemas. A habilidade de narrar é específica do ser humano, pelo que se optou pela apresentação oral, pelos grupos, dos seus avatares e discussão com a turma relativamente ao enunciado. Além disso, foram selecionados jogos interativos, on-line, relativos à tabuada, para consolidação e mais facilmente resolveres problemas. Finalizou-se com a criação de um livro on-line que pretendia sistematizar, em forma de esquema ou de texto (os alunos é que decidiam) o que tinham aprendido ao longo do projeto. A Tabela 1 permite compreender as estratégias e impactos (Tabela1).

Reforça-se que através do uso do computador, utilizou-se uma aplicação on-line Voki (criação de avatares). Foi possível constatar-se que o facto da criança ter de pensar no enunciado, escrevê-lo ou ditá-lo na aplicação, fez com que os alunos tomassem consciência da linguagem matemática e da necessidade de esta ser rigorosa. Além disso, foi possível aferir que entenderam que, da mesma forma que na primeira etapa do método de Polya precisam de descobrir os dados no enunciado, ao formular problemas também precisam de descobrir os dados para colocar no enunciado, para que este tenha sentido. Ora, nas situações formativas anteriores ao trabalho com os avatares, os alunos não sabiam com exatidão como criar um enunciado e o que nele era preciso conter.

Na verdade, o uso do computador e das aplicações mencionados permitiu aos alunos consolidar os conteúdos abordados de uma forma diferente, tomando consciência das suas aprendizagens, nomeadamente das características necessárias de um enunciado, quer na formulação de problemas quer na resolução de problemas. O facto de criarem textos, esquemas mensagens escritas e audíveis, com recurso às tecnologias, fez com que os alunos reconhecessem as suas dificuldades de literacia e encontrassem soluções no seio do grupo, encarando as dificuldades numa perspetiva positiva, tentativa e erro e não derrotadora.

7. Considerações Finais

Recorrer à gamificação e ao método de Polya como estratégias de melhoria do desempenho dos alunos na resolução de problemas com a operação da divisão permitiu-nos concluir que é uma união relevante no processo de ensino e aprendizagem, pois não só estimulou a integração de saberes, como também fomentou a fórmula “ensinar a técnica” + “realizar já tarefa” num ambiente prazeroso estimulando o apender a fazer fazendo com satisfação. Estamos perante um processo de reconstrução onde a experimentação é valorizada, o erro torna-se menos relevante na fala dos avatares, a articulação curricular nasce de forma natural e as soluções encontradas tornam-se mais significativas para o grupo. Além disso, os resultados revelam que o método Polya ajudou a melhor compreender e organizar o problema fomentando autonomia na resolução do problema, que a gamificação estimulou o entusiasmo e o desejo de os grupos atingirem os seus objetivos e que recursos digitais no processo de ensino aprendizagem motivaram os alunos na aprendizagem aumentando o desejo de realizar exercícios, mas também a construção de avatares pelos alunos promoveu uma melhor consciencialização da formulação de problemas.

Recorrendo a propriedades e regras do jogo, o uso das tecnologias (e dos vários programas utilizados), a história que acompanhou o projeto, o cenário, os desafios contextualizados e o trabalho colaborativo, foram estratégias pensadas pela professora estagiária, com o fim de motivar os alunos para a construção das suas aprendizagens. Desta forma, ao mesmo tempo que aprendiam a ultrapassar as dificuldades, aprendiam novos conhecimentos e reconstruíam outros. Na verdade, para responder ao objetivo geral foi desenvolvida uma articulação de duas áreas mais específicas, nomeadamente a matemática e o português. Repare-se que ao criar enunciados, ao criarem avatares e o livro online, os alunos desenvolveram competências de escrita e de interpretação de texto, assim como desenvolveram competências de oralidade, na criação de mensagens audíveis. Estas competências foram desenvolvidas nos textos-síntese que os alunos iam criando, bem como no esquema criado no livro on-line. Desenvolveu-se, também, o domínio da leitura, com a leitura da história que acompanhava todas as situações formativas. Esta articulação de saberes, cada vez mais valorizada no ensino, foi fulcral para tornar as aprendizagens dos alunos mais significativas. De uma forma geral, a gamificação influenciou positivamente a atitude dos alunos em relação aos conteúdos matemáticos e à própria disciplina, o método de Polya fez com que os alunos se tornassem mais autónomos na resolução de problemas e o uso de recursos digitais ajudaram os alunos a tomarem consciência das características do enunciado. Pelo exposto, considera-se que aliar o método de Polya à gamificação acrescenta valor à capacidade de alunos responderem com mais eficiência a tarefas que envolvam a resolução de problemas matemáticos.

Referencias bibliográficas

Amador, M. (2018). La gamificación como estrategia educativa. http://www.formacionib.org/noticias/?La-gamificacion-como-estrategias-educativa.

Andrade, F., Quadros-Flores, & Pinto, J. (2019). Gamification as a strategy for promoting child involvement: A study on spatial orientation in the 1st CEB. International Journal of Advanced Engineering Research and Science (IJAERS) 6(11) 399-411. https://dx.doi.org/10.22161/ijaers.611.62.

Almeida, L. & Freire, T. (2000). Metodologias da Investigação em Psicologia e Educação. Braga: Compolito, Lda.

Bogdan, R. & Biklen, S. (1994). Investigação Qualitativa em Educação. Porto: Porto Editora.

Carmo, H. & Ferreira, M. (2008). Metodologia da Investigação – Guia para Auto-aprendizagem. Lisboa: Universidade Aberta.

Casaril, M. (2016). Programa Internacional de Avaliação de Estudantes (PISA): a concepção de letramento e o estado da arte no Brasil. Trama, 12(27), 84-109.

Chou, Y. K. (2016). Actionable Gamification: Beyond Points, Badges, and Leaderboards. Canada: Leanpub.

Deterding, S., Sicart, M., Nacke, L., O’Hara, K., & Dixon, D. (2011). Gamification. using game-design elements in non-gaming contexts. In CHI’11 extended abstracts on human factors in computing systems (pp. 2425-2428). Vancouveger, Canadá. ACM 978-1-4503-0268-5/ 11/ 05.

Fardo, M. L. (2013). A gamificação aplicada em ambientes de aprendizagem. RENOTE, Revistas Novas tecnologias na Educação, 11(1)1-9. ISSN 1679-1916. https://doi.org/10.22456/1679-1916.41629.

Kapp, K. M. (2012). The gamification of learning and instruction: game-based methods and strategies for training and education. Conjectura: Filos. Educ., Caxias do Sol 18 (1), 201-206.

Krulik, S. & Reys, R. (Eds.). (1980). Problem solving in school mathematics. Reston: NCTM.

Latorre, A. (2003). La investigación-acción: Conocer y cambiar la práctica educativa (3ªed). Barcelona: Graó.

Martinho, H. (2011). A comunicação na sala de aula de matemática: um projecto colaborativo com três professoras do ensino básico. Braga: Centro de Investigação em Educação. Instituto de Educação e Psicologia da Universidade do Minho.

Marôco, J. (coord.), Gonçalves, C., Lourenço, V., & Mendes, R. (2016). PISA 2015-Portugal: Literacia Científica, Literacia de Leitura & Literacia Matemática. Lisboa: Instituição de Avaliação Educativa.

Mascarenhas, D., Maia, J., & Martínez, T. S. (2017). Geometria e Grandezas no 5º ano: Dificuldades e Estratégias – Um Estudo em duas escolas do distrito do Porto. Berlin: Novas Edições Académicas.

Meirinhos, M. & Osório, A. (2010). O estudo de caso como estratégia de investigação em educação. EDUSER: Revista de Educação, 2 (2), 49-65.

Monteiro, I. (2018). No futuro se faz presente! Tese de Mestrado. Porto: Escola Superior de Educação do Politécnico do Porto.

Polya, G. (1977). A arte de resolver problemas. Rio de Janeiro: Editora Interciência.

Polya, G. (1980). On solving mathematical problems in high school. In S. Krulik & R. Reys (Eds.), Problem solving in school mathematics (pp. 1-2), Reston: NCTM.

Polya, G. (2003). Como resolver problemas. Lisboa: Gradiva.

Ponte, J. P. (2005). Gestão curricular em Matemática. In GTI (Ed.), O professor e o desenvolvimento curricular (pp. 11-34). Lisboa: APM.

Richter, G., Raban, D. R., & Rafaeli, S. (2015). Studying gamification: the effect of rewards and incentives on motivation. In Gamification in education and business (pp. 21-46). Springer, Cham.

Sampaio, E. (2018). Nunca é tarde para aprender. Tese de Mestrado. Porto: Escola Superior de Educação do Politécnico do Porto.

Windham, D. M. (1990). Declaração Mundial sobre Educação para Todos: Satisfação das Necessidades Básicas de Aprendizagem. Jomtien: UNESCO. https://unesdoc.unesco.org/search/N-EXPLORE-a882e630-f046-4e40-bcae c614df59801d.

Vale I. & Pimentel, T. (2004). Resolução de problemas. In P. Palhares (coord.). Elementos da matemática para professores do ensino básico. Lisboa: Lidel.

Vassileva, J. (2012). Motivating participation in social computing applications: a user modeling perspective. User Modeling and User-Adapted Interaction, 22(1-2), 177-201.

Zichermann, G., & Cunningham, C. (2011). Gamification by design: Implementing game mechanics in web and mobile apps. O’Reilly Media, Inc. https://dl.acm.org/citation.cfm?id=2073550.

Zichermann, G., & Linder, J. (2010). Game-based marketing: inspire customer loyalty through rewards, challenges, and contests. https://www.wiley.com/enus/Game+Based+

Marketing%3A+Inspire+Customer+

Loyalty+Through+Rewards%2C+

Challenges%2C+and+Contests+

-p-9780470562239.