YVETH ALBORNOZ CARHUATANTA
Universidad Nacional Mayor de San Marcos, Perú.
yveth33@gmail.com
ORCID 0000-0002-1371-0242
RESUMEN:
El presente estudio está enmarcado en el empleo de Estrategias Resolutivas de Allan Schoenfeld para la solución de problemas matemáticos de alta demanda cognitiva. El tipo de investigación fue descriptiva correlacional con un diseño pre-experimental longitudinal. La población estuvo conformada por 70 estudiantes entre dos secciones de cuarto año de secundaria de un colegio ubicado en Lima Metropolitana la cual fue tomada en su totalidad. En lo que respecta a las técnicas se utilizó la encuesta y como instrumentos un cuestionario para recolectar los datos sociodemográficos tales como el sexo y edad. Adicionalmente, se aplicó una Prueba de Conocimientos Previos en conceptos matemáticos, una Prueba de Problemas de Contexto elaborada con base en la prueba Pisa aplicadas años atrás que buscó medir las estrategias resolutivas empleadas en la solución de dichos problemas y tres instrumentos para recoger la valoración de los estudiantes sobre las estrategias heurísticas, estrategias metacognitivas y creencias en relación al curso. Los instrumentos fueron validados a través del juicio de expertos y se obtuvo un índice de Osterlind de 0.75. En cuanto a la confiablidad, tuvieron un alfa de Cronbach por encima del 0.80 para cada uno. La metodología que se utilizó fue la aplicación de sesiones de aprendizaje con diversas situaciones problemáticas empleadas para la preparación a las pruebas Pisa, estas presentan 4 secciones: conexiones, herramientas matemáticas, matemática en contexto y manos a la obra. Las pruebas y cuestionarios fueron aplicados antes y después de la totalidad de realización de las sesiones. Los resultados mostraron que luego de la intervención pedagógica, los estudiantes mejoraron con cierto nivel de significatividad su capacidad para resolver problemas y probando la hipótesis que existe relación entre algunas de las estrategias resolutivas según la propuesta de Allan Schoenfeld y la solución de problemas matemáticos de alta demanda cognitiva.
PALABRAS CLAVE: Intervención pedagógica, problemas matemáticos, estrategias resolutivas, alta demanda cognitiva, prueba de contexto, conocimientos previos estrategias heurísticas, estrategias metacognitivas, creencias en relación al curso.
ABSTRACT:
Allan schoenfeld's solution strategies and the solution of mathematical problems of high cognitive demand
The present study is framed in the use of Allan Schoenfeld's Solution Strategies for the solution of mathematical problems of high cognitive demand. The type of research was descriptive correlational with a pre-experimental longitudinal design. The population consisted of 70 students between two sections of fourth year of high school in a school located in Metropolitan Lima, which was taken in its entirety. Regarding the techniques, the survey was used and the instruments used was a quiz to collect sociodemographic data such as sex and age. Additionally, a Test of Previous Knowledge of mathematical concepts, a Test of Contextual Problems based on the Pisa test applied years ago, which seeks to measure the solution strategies used in the solution of these problems, and three instruments to collect the students' evaluation of heuristic strategies, metacognitive strategies and beliefs in relation to the course were applied. The instruments were validated through expert judgment and an Osterlind index of 0.75 was obtained. In terms of reliability, they had a Cronbach's alpha above 0.80 for each one. The methodology that was used the application of learning sessions with various problematic situations used to prepared for the Pisa test, these present 4 sections: connections, mathematical tools, mathematics in context and hands to work. The test and questionnaires were applied before and after the totality of the sessions. The results showed that after the pedagogical intervention, the students improved with certain level of significance their ability to solve mathematical problems and proved the hypothesis that there is a relationship between some of the solving strategies according to Allan Schoenfeld's proposal and the solution of mathematical problems of high cognitive demand.
KEYWORDS: Pedagogical intervention, math problems, resolution strategies, high cognitive demand, context test, Previous Knowledge, heuristic strategies, metacognitive strategies, beliefs in relation to the course.
1. Introducción
Desde muchos años, existe una creciente preocupación ya generalizada porque la resolución de problemas sea una actividad del pensamiento como resultado del análisis - razonamiento y no una mera aplicación repetitiva y mecánica de algoritmos con la única intención de obtener un resultado sin el debido tiempo de razonar si dichos procedimientos responden a la solución del problema (Prendergast et al., 2018; Lane et al., 2016; Gijsbers et al., 2019). En la mayoría de los casos se ve que se trata de una mera aplicación de algoritmos repetidos sin operacionalizar las situaciones problemáticas de la vida real donde se pueda medir las competencias interpretativas y argumentativas de las mismas. Asimismo, también se requiere ser capaces de elegir las estrategias heurísticas adecuadas que busquen la iniciativa, la concentración, la creatividad y la seguridad por encontrar el resultado tras un trabajo de análisis y raciocinio (Hammad et al., 2020; Klymchuk, 2017; Kitchen, 2020).
El verdadero reto de la educación matemática en la resolución de problemas es que los estudiantes ejecuten acciones haciendo uso de estrategias y conceptos matemáticos que ya poseen ampliando de esta manera sus conocimientos y estrategias, así lo señala el Ministerio de Educación en el documento Rutas de aprendizaje (2009) …el desempeño eficaz de la matemática está asociado con la capacidad de resolver problemas, ya que mediante esta actividad se introducen nuevos conceptos, se ponen en uso los aprendidos o se realizan conexiones entre estos para formar redes conceptuales más amplias… (p.49) (Radmehr & Drake, 2018; Schoen et al., 2019).
Esta necesidad latente se ha expresado en muchos países del mundo, quienes buscan tener estudiantes cada vez más competentes para enfrentarse a diversas situaciones propias de su entorno donde no solo sean capaces de aplicar los conocimientos aprendidos, sino que también sepan elegir una o más estrategias que le lleven a la solución del problema que enfrentan (Jäder, et al., 2019; Olivares et al., 2020).
Ante esta situación, diversas entidades educativas han creado evaluaciones internacionales que buscan medir las competencias y capacidades que adquirieron los estudiantes y qué medidas se deben adoptar para mejorar o seguir en la mejora (Tsai & Li, 2017).
En el marco de este trabajo de investigación, se enfatizará en los resultados de la competencia matemática la cual está definida como la capacidad del individuo para formular, emplear e interpretar las matemáticas en una variedad de contextos lo cual incluye el razonamiento matemático y la utilización de conceptos, procedimientos, datos y herramientas matemáticas para describir, predecir y explicar fenómenos (Kitchen, 2020; Gijsbers et al., 2019). También se buscará resaltar y reconocer en los interesados (estudiantes, profesores y sociedad en general) el rol que desempeña las matemáticas en el mundo y a emitir juicios y decisiones bien fundadas requeridos por los ciudadanos constructivos, comprometidos y reflexivos (Kitchen, 2020).
En el marco de las evaluaciones internacionales, se resalta la resolución colaborativa de problemas la cual comprende como la capacidad de una persona para implicarse de forma eficaz en un proceso en el que dos o más participantes intentan resolver un problema compartiendo la comprensión y el esfuerzo necesario para llegar a una solución y mancomunar conocimientos, destrezas y esfuerzos para este fin. (PISA, 2015; Hammad, et al., 2020). Dicha competencia busca desarrollar en los estudiantes la habilidad para comprometerse efectivamente en un proceso en el que dos o más individuos intentan resolver un problema agrupando sus conocimientos y habilidades para alcanzar una solución. Como educadores, sabemos que cuando los estudiantes se encuentran en equipos de trabajo, pueden compartir sus conocimientos, estrategias y habilidades, pueden socializar las posibles rutas de solución y sobre todo pueden apoyarse ante las limitaciones de alguno de los integrantes. La solución a un problema de contexto real, no siempre surge del pensamiento de un individuo sino del trabajo en conjunto. (Jäder, et al., 2019; Guven et al., 2016).
Desde hace varios años, el Ministerio de Educación ha venido implementando el Currículo Nacional de Educación Básica (CNEB) de acuerdo a los estándares a nivel mundial donde se plantea trabajar una matemática para y desde la vida, desarrollando desempeños y capacidades, creando nuevos aprendizajes a partir de situaciones significativas contextualizadas a su entorno, con datos reales y de interpretación crítica (Shahbari, 2017). En ese sentido, se quiere desarrollar la competencia matemática en un sentido más significativo y real para el estudiante; y busca orientar su enseñanza aprendizaje bajo el enfoque centrado en la resolución de problemas, es decir, lo que se busca es plantear problemas que consideren el contexto sociocultural del estudiante; que deben partir de ejemplos concretos de su entorno de manera que pueda sentirse familiarizado y de este modo le permita pensar crítica y analíticamente en la solución de los mismos con ayuda de las herramientas que ya posea o de aquellos que pueda ir encontrando en su camino de resolución. (Tisdell, 2019; Kitchen, 2020).
Conocido los resultados obtenidos en las evaluaciones PISA por nuestros estudiantes en los últimos años y conocidas las orientaciones del MINEDU sobre la importancia y la necesidad de enseñar a partir de problemas contextualizados, se considera imprescindible conocer también los resultados de la evaluación diagnóstica de la población de estudio para este trabajo de investigación comprendida por estudiantes del 4to año del nivel secundario de un colegio ubicado en el distrito de Magdalena del Mar de Lima Metropolitana.
En cuanto al área de matemática, hace algunos años atrás, los estudiantes que egresaban tenían serias deficiencias en cuanto a la resolución de problemas, esto se debía a que los docentes se habían dedicado a trabajar la parte operativa, los algoritmos y propiedades, dejando de lado la resolución de situaciones problemáticas contextualizadas y el manejo de estrategias heurísticas (Jäder, et al., 2019; Olivares et al., 2020).
Asimismo, trabajaban con un material escolar que sólo desarrollaba procedimientos, repetición de algoritmos y aplicación directa de propiedades, que, sin quitarle méritos, logro darles un buen nivel académico operativamente hablando que en la misma línea que Jäder et al., (2019) sus contenidos así como la forma de presentar las oportunidades de aprendizaje estaban disponibles para los estudiantes siendo este material la base de la instrucción. No obstante, no había una clara distinción entre si el estudiante debía comprometer su comprensión o simplemente producir una respuesta haciendo énfasis en los indicadores de las soluciones, como las palabras clave, las preguntas de orientación y los procedimientos paso a paso que hay que memorizar, conduciendo a los estudiantes a la resolución de tareas basadas en las habilidades, sin un énfasis serio en la comprensión (Jäder et al., 2019).
El presente trabajo busca enriquecer la praxis docente con el desarrollo de las competencias matemáticas, desempeños y capacidades, como es la resolución de problemas, punto débil aún de nuestro sistema educativo. Es decir, lo que se busca en el estudiante es que emplee formas de razonamiento matemático que sea independiente del docente u otra figura de autoridad; sea capaz de crear sus propias conjeturas y explorar su validez; y despertar y mantener una actitud escéptica sobre las propiedades matemáticas (Campbell et al., 2019).
El Minedu ha venido enfatizando la importancia de trabajar la matemática desde un punto no solo procedimental sino a nivel de competencias y desempeños diversificados en situaciones problemáticas contextualizadas (Guven, et al., 2016). Exige que los estudiantes aprendan a interactuar de manera creativa, autónoma, autorregulada y responsable con la gran cantidad de conocimientos que aprenden diariamente, demandando a la escuela y mucho más a los docentes, la enseñanza de estrategias diversas que los ayuden a resolver problemas en diversos contextos a partir de procesos conscientes y regulados, es decir, a partir de la reflexión de sus propios procesos cognitivos (Metacognición) (Olivares et al., 2020; Monarrez & Tchoshanov 2020).
En ese sentido, los profesores para Kitchen, (2020) deben crear entornos en los que los estudiantes se involucren activamente en la práctica de las matemáticas para establecer conexiones entre los diferentes hechos matemáticos y algoritmos (Coskun & Bostan, 2018; Tisdell, 2019; Kontorovich, 2019; Olivares et al., 2020).
Asimismo, se requiere trabajar en las estrategias resolutivas para la solución de problemas de alta demanda cognitiva (utilizado en las evaluaciones de PISA) y comprobar si factores como los conocimientos previos, las estrategias heurísticas, las estrategias metacognitivas y las creencias en relación al curso de matemática presentan alguna relación. En ese sentido, las creencias de los estudiantes inciden sobre sus motivaciones (por ejemplo, la autoconciencia, la autoeficacia, la orientación hacia los objetivos y la actitud) en lo que la actitud hacia el aprendizaje de una asignatura tiene un fuerte impacto en el aprendizaje y el rendimiento. Por ejemplo, los estudiantes con una mentalidad de crecimiento atribuyen el éxito al esfuerzo, tienden a tener más resiliencia ante el fracaso y demuestran más perseverancia en las tareas difíciles que los estudiantes que atribuyen el éxito a la capacidad por lo que resalta la importancia que el estudiante sea consciente de su propio posicionamiento en relación con el aprendizaje de un tema o asignatura (Norqvist, 2018; Shahbari, 2017; Raveh & Shaharabani, 2019; Radmehr & Drake, 2018).
Se ha podido observar que en nuestra población de estudio existe una carencia en el desarrollo de estrategias resolutivas de problemas y mucho más aquellas que respondan a la solución de problemas de alta demanda cognitiva. De allí la importancia que los docentes planifiquen y programen las tareas con sumo cuidado para ayudar a los estudiantes a comprender la idea o el concepto matemático correspondiente. También debe tomarse en cuenta que la elección de una actividad pedagógica está en consonancia con los contenidos matemáticos que el propio docente posee y mientras más robusto sea el corpus teórico de conocimientos matemáticos de este, más tenderá a elegir e implementar tareas con alta demanda cognitiva. (Coskun & Bostan, 2018; Norqvist, 2018; Shahbari, 2017; Raveh & Shaharabani, 2019; Olivares et al., 2020; Hong & Choi, 2019; Monarrez & Tchoshanov 2020).
Por lo antes expuesto, el presente estudio tuvo como objetivodeterminar si existe relación entre las estrategias resolutivas según la propuesta de Allan Schoenfeld y la solución de problemas matemáticos de alta demanda cognitiva en estudiantes de nivel secundario de un colegio ubicado en el distrito de Magdalena del Mar de Lima Metropolitana. Para ello se considerarán las relaciones entre las dimensiones: conocimientos previos, estrategias heurísticas, estrategias metacognitivas, creencias en relación al curso y la solución de problemas matemáticos de alta demanda cognitiva.
2. Metodología
El presente trabajo de investigación está enmarcado en los criterios metodológicos del paradigma cuantitativo, con un diseño de tipo cuasi-experimental. El resultado es la valoración del cambio ocurrido desde la aplicación de los cuestionarios, la prueba de conocimientos, la prueba sobre problemas de contexto real aplicados antes y después de las 8 sesiones sobre estrategias y resolución de problemas.
Este diseño se muestra en el siguiente gráfico:

Se inició con un grupo de 70 estudiantes (E), a los cuales aún no se le ha aplicado ningún tratamiento (No R), se procede a aplicar los primeros instrumentos de recojo de datos como los cuestionarios y pruebas iniciales (O), después de ello se aplica el tratamiento que comprende 8 sesiones (X) para finalmente, volver a recoger datos con los instrumentos iniciales (O) para ver si se logró cumplir los supuestos planteados. Se pretende medir los cambios que se producen, a lo largo de un tiempo (8 semanas), en la misma muestra de individuos y contrastar las diferencias interindividuales en los cambios intraindividuales.
La población objeto de estudio está conformada por los estudiantes de cuarto año de secundaria de la Educación Básica Regular matriculados en el año 2019 de un colegio ubicado en el distrito de Magdalena del Mar de Lima Metropolitana. Los estudiantes se encuentran divididos en dos grupos: el A con 34 estudiantes (25 varones y 9 mujeres) y B con 36 estudiantes (25 varones y 11 mujeres) dando una población total de 70 alumnos comprendidos entre 15 y 16 años. La población de estudio no tuvo condiciones especiales de aprendizaje. Por otra parte, en virtud del tamaño poblacional esta fue tomada en su totalidad por lo que no fue necesario el cálculo del tamaño de la muestra ni utilizar técnicas de muestreo.
2.1. Técnicas e instrumentos de recolección de datos
Los instrumentos utilizados fueron sometidos a la validez de contenido a través del juicio de expertos quienes hicieron las observaciones pertinentes. En ese sentido, el cuestionario sobre Estrategias Heurísticas estuvo conformado con 31 ítems y después de las observaciones la versión final quedó con 27. El instrumento para medir las estrategias Metacognitivas tuvo originalmente 38 y la versión final quedó con 35 ítems. Por último, el cuestionario para medir las Creencias en relación al curso tuvo originalmente 38 ítems y la versión final quedó con 33. Paralelamente, se hizo el cálculo del índice de Osterlind cuyo promedio general fue de 0.75.
Con relación a la confiablidad, se obtuvo del alfa de Cronbach para cada uno de los instrumentos el cual fue de ,894 para el cuestionario Estrategias Heurísticas, ,902 para el cuestionario Estrategias Metacognitivas y ,819 para el cuestionario Creencias en relación al curso.
Se utilizó la técnica de la encuesta y como instrumento cuestionarios cuya medición fue por escalas expresados en 4 niveles para el recojo de información sobre las estrategias y creencias. Para los conocimientos previos y la medición sobre resolución de problemas matemáticos se utilizaron pruebas calificadas con una escala vigesimal. Vale la pena resaltar el hecho de que la cantidad de instrumentos utilizados va en consonancia con el modelo propuesto por Allan Schoenfeld el cual contempla las estrategias heurísticas, estrategias metacognitivas, creencias con relación al curso y las pruebas de conocimientos previos. A continuación, detallamos cada uno de ellos:
La Prueba de Problemas de Contexto, la cual fue elaborada con 9 situaciones problemáticas extraídas de evaluaciones Pisa aplicadas años atrás que busca medir el nivel alcanzado en cuanto a las estrategias resolutivas empleadas por los estudiantes en la solución de problemas matemáticos. Los problemas matemáticos seleccionados para esta puesta en práctica no son del tipo de textos escolares sino aquellos que utilizó el Ministerio de Educación en la preparación de los estudiantes participantes en la evaluación PISA (2015). Además, estos problemas fueron seleccionados considerando su contextualización, sus conexiones matemáticas y las diversas estrategias que necesitaban para su resolución. Las hipótesis buscan verificar la posible relación de dichas estrategias con la solución de problemas matemáticos serán probadas en el entendido que el p-valúe sea menor al nivel de significancia de 0,05.
Una Prueba de Conocimientos Previos en conceptos matemáticos, la cual consistió en una evaluación con 13 ítems que ayudó a recoger información previa sobre conceptos, procedimientos, propiedades y fórmulas matemáticas necesarias para resolver los problemas que se desarrollarían en las sesiones de clase. Para resolver problemas matemáticos es necesario tener una badaje bien estructurado de conceptos y definiciones que permitan aplicarse en el proceso de solución. Por ejemplo, si se nos pide calcular el área pero no se conoce la fórmula matemática de la forma geométrica en cuestión, entonces no se podrá avanzar en la solución de la situación planteada.
Las pruebas anteriormente mencionadas fueron evaluadas en la escala vigesimal (0-20). No obstante, los resultados fueron agrupados según el baremo En Inicio (0-10), En proceso (11-15) y Logrado (16-20) de acuerdo a los niveles de logro que desarrolla actualmente nuestro sistema educativo y para realizar un mejor tratamiento estadístico.
Por otra parte, se aplicó un cuestionario para recoger la valoración de los estudiantes sobre las estrategias heurísticas, el cual estuvo constituido por las dimensiones Conocimiento de las estrategias (9 ítems) y Utilización de las estrategias (17 ítems) para un total de 26 ítems. Con este instrumento, se midieron las competencias de los estudiantes, en el antes y después de la intervención pedagógica, sobre cuánto y qué estrategias conocen y utilizan para resolver los problemas matemáticos. El manejo y dominio de estrategias heurísticas define el proceso resolutivo que utilizará para encontrar la respuesta correcta, permite que utilice dos o más estrategias cuando sea necesario y que no se quede atrapado en el mismo procedimiento por mucho tiempo.
El cuestionario de estrategias metacognitivas estuvo constituido por las dimensiones Conocimiento de la metacognición (17 ítems) y Regulación de la metacognición (18 ítems) con un total de 35 reactivos. Con este, se buscó medir los procesos metacognitivos que, en la solución de problemas, cumplen una función autorreguladora que permite al estudiante reflexionar sobre los procesos que realiza al resolver problemas: el estudiante debe revisar los conocimientos previos que posee para entender el problema, debe analizar, seleccionar y planificar la estrategia a utilizar, la cual se encuentra estructurado en su mente y representado en el papel, todo esto debe realizarlo en cada momento del proceso resolutivo.
Por último, el cuestionario sobre creencias en relación al curso de matemática se elaboró considerando las dimensiones: Creencias en relación a los docentes (13 ítems), Creencias de los estudiantes (12 ítems) y Creencias en relación al curso propiamente dicho (8 ítems) para un total de 33 ítems. Con este instrumento se recogió información sobre las creencias de los estudiantes, dado que estas condicionan qué tan dispuestos están los estudiantes para trabajar en Matemática y mucho más conocer las ideas y actitudes que asumen cuando deben enfrentarse a un problema matemático.
Los ítems de estos cuestionarios sean han elaborado empleando la escala Likert, cuya escala de medición es ordinal con cuatro opciones de respuesta: (1) completamente en desacuerdo, (2), en desacuerdo, (3) de acuerdo y (4) completamente de acuerdo. No obstante, para los efectos del análisis y de acuerdo a los resultados obtenidos, estos fueron agrupados en niveles bajo, medio y alto a partir del cual se midió el impacto de las estrategias resolutivas de Allan Schoenfeld en la solución de problemas matemáticos de alta demanda cognitiva.
De acuerdo con la prueba de normalidad de Kolmogorov-Smirnov los datos no siguen una distribución normal (p<0.05) por lo que utilizó pruebas no paramétricas. Para establecer la relación entre las estrategias resolutivas de Allan Schoenfeld y la solución de problemas matemáticos de alta demanda cognitiva se utilizó el coeficiente de Spearman. Para el caso de la prueba de conocimientos previos, estrategias heurísticas, estrategias metacognitivas y creencias en relación al curso; y las pruebas de contexto, se utilizó la prueba de Wilcoxon para datos apareados que permitió comparar la diferencia de las medias del grupo antes y después de la intervención pedagógica y corroborar si estas cumplieron su propósito, o no, para una significancia de 0,05.
3. Resultados
3.1. Análisis demográfico
Con relación a las características sociodemográficas de los estudiantes, la población de cuarto año de secundaria estuvo constituida en su mayoría por varones con el 74.3% (50) mientras que las mujeres representaron el 25.7% (18). La diferencia entre ambos géneros se debe a que la institución educativa desde sus inicios estuvo conformada por la totalidad de estudiantes varones y desde hace 10 años se convirtió en un colegio mixto (solo permiten que el 25% de estudiantes por aula sean mujeres). Además, la media de la edad de los estudiantes fue de 14.8±0.40 años. Es importante señalar que la mayoría de los individuos de la población en este estudio cuentan con los medios y recursos necesarios para lograr un aprendizaje significativo, que provienen de familias constituidas por ambos padres así como también de familias disfuncionales.
3.2. Análisis de los resultados del puntaje obtenido en la Prueba de conocimientos previos (AIP - DIP) y la Prueba de Contexto (AIP - DIP)

Tabla 1. Medidas de Resumen de los puntajes de la Prueba de Conocimientos Previos
En la tabla 1, se observa que la media (11,74) del puntaje de la prueba de conocimientos previos después de la intervención pedagógica es mayor que antes (8,94). Es decir, que los estudiantes han mejorado sus conocimientos previos sobre matemática, aunque el avance de lo aprendido es homogéneo en consideración a sus respectivas medias.
La media (12,9) del puntaje de la prueba de Contexto después de la intervención es mayor que antes (8,91) de la intervención y la dispersión no varía tanto. Es decir, que los estudiantes si lograron elevar su nivel de logro para resolver problemas matemáticos de contexto, aunque el avance de lo aprendido es también homogéneo en consideración a sus respectivas medias. Es preciso enfatizar que esta pequeña mejoría de las medias si permite señalar un nivel de relación entre las variables en estudio.
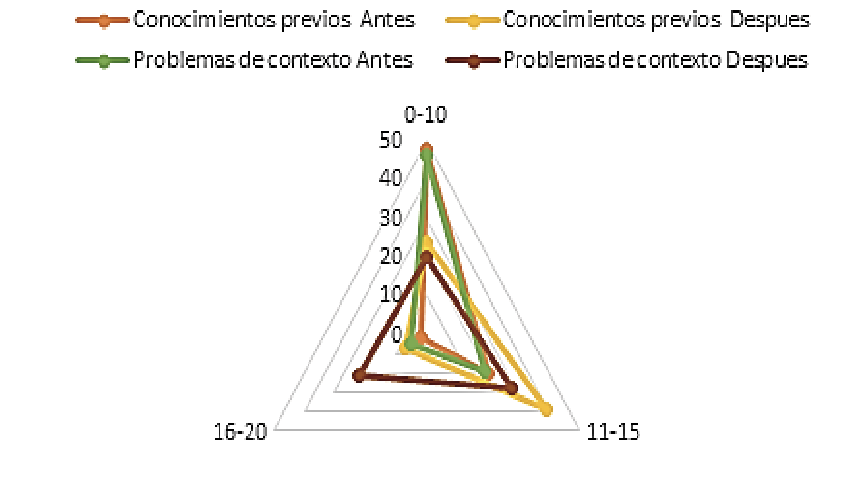
Figura 1. Resumen de los resultados de acuerdo con la escala de desempeño
Al baremizar los resultados tanto de la prueba de conocimientos previos como la de la prueba de contexto de acuerdo a la escala descrita en la sección de métodos para estos instrumentos (bajo, medio y alto) se aprecia en la figura 1 que hubo una mejoría en el desempeño de los estudiantes al pasar del nivel de En inicio (antes un 68,8%) a los niveles de En proceso y Logrado con 55,7% y 10% respectivamente obteniéndose En Inicio solo un 34,3%. Igual escenario se presentó con la prueba de contexto que pasó de estar En Inicio (antes un 65,7%) a los niveles En Proceso y Logrado con 40% y 31,4% respectivamente, obteniendo solo un 28,6% de los estudiantes en el nivel En Inicio. A partir de estos resultados se puede afirmar que la mayoría de los estudiantes lograron pasar al siguiente nivel de logro esperado respecto al cual se encontraban antes de la intervención pedagógica demostrando la relación de los conocimientos previos en el área y la solución de problemas matemáticos.
Además, los conocimientos previos antes y después de la aplicación de las estrategias resolutivas, para cada estudiante con diseño apareado se verificó si las diferencias de los puntajes, tenían distribución de probabilidad normal, verificándose con p-valor < 0.05 que la muestra de diferencias por pares de datos, no tiene distribución normal de probabilidad, impidiendo el empleo de la prueba estadística t de Student para datos apareados. Por tanto, se empleó la prueba no paramétrica de rangos con signo de Wilcoxon para este diseño, el p-valor obtenido fue menor al supuesto (p-valor<0.05) rechazando la hipótesis de nulidad que las estrategias resolutivas propuestas de Allan Schoenfeld sobre conocimientos previos no tiene efecto, con 5% de nivel de significación se concluye que estas estrategias se relacionan con la resolución de problemas matemáticos (prueba de contexto).
Por otra parte, la prueba de rangos con signo de Wilcoxon determinó que existe significancia estadística entre las pruebas de conocimientos previos hecha en el antes y después de la aplicación de las estrategias resolutivas de Allan Schoenfeld para la resolución de problemas matemáticos de alta demanda cognitiva dado que el p-valor obtenido fue menor al supuesto (p-valor<0.05). Igual escenario se presentó entre las pruebas de contexto hechas en el antes y después de la aplicación de las estrategias resolutivas de Allan Schoenfeld para la resolución de problemas matemáticos de alta demanda cognitiva.
3.3. Análisis de los resultados del puntaje obtenido en los cuestionaros Estrategias Metacognitivas, heurísticas y creencias con relación al curso (AIP - DIP) y la Prueba de Contexto (AIP - DIP)
En la figura 2 se aprecian los resultados de los cuestionarios estrategias heurísticas, creencias con relación al curso y estrategias metacognitivas y puede verse que, según el baremo empleado en cada una de ellas se obtuvo una tendencia hacia el nivel medio en el después de la aplicación de las estrategias resolutivas de Allan Schoenfeld.
Para el caso de las estrategias metacognitivas, los resultados sugieren que la mayoría de estudiantes se ubicaron en el nivel medio con un 84,3% (antes se obtuvo 62,9%) mientras que en el nivel alto se obtuvo solo un 7,1%. Es decir, se observa que la mayoría de estudiantes se ubicó en el nivel medio, verificándose un ligero incremento de estudiantes en este nivel de aquellos que estuvieron ubicados inicialmente en el nivel alto.
Con relación a las creencias en relación al curso, los resultados de la figura 2 sugieren que mantuvo la tendencia mayoritaria de estudiantes en el nivel medio en el después de la aplicación de las estrategias resolutivas de Allan Schoenfeld. En términos numéricos estos resultados muestran que la mayoría de los estudiantes se ubicaron en los niveles medio y alto con 75,7% y 12,9% respectivamente (antes se obtuvieron 65,7% y 10%). Es decir, se observa un ligero incremento de estudiantes en ambos niveles de logros esperados y en la percepción de los mismos en torno a las creencias que consideran son de interés y que pueden ser determinantes cuando se quiere resolver problemas matemáticos.
Con relación a las estrategias heurísticas, los resultados de la figura 2 sugieren que mantuvo su tendencia mayormente en el nivel medio en el después de la aplicación de las de las estrategias resolutivas de Allan Schoenfeld en donde, además, se aprecia un incremento en el nivel alto. En términos numéricos, estos resultados muestran que la percepción con relación a las estrategias heurísticas de los estudiantes no hubo variación en el nivel bajo en ambos momentos de la intervención y se obtuvieron resultados similares (18,5%). En el nivel medio y alto se obtuvieron 68,6% y 12,9% respectivamente después de la intervención pedagógica remarcando que en el nivel medio se había obtenido en el antes un 71,4%. A partir de estos resultados podemos inferir que un pequeño porcentaje de estudiantes lograron pasar del nivel medio al nivel alto destacándose una mejora en su manejo y dominio de estrategias heurísticas mientras que en la mayoría no se pudo reflejar dicha mejoría.
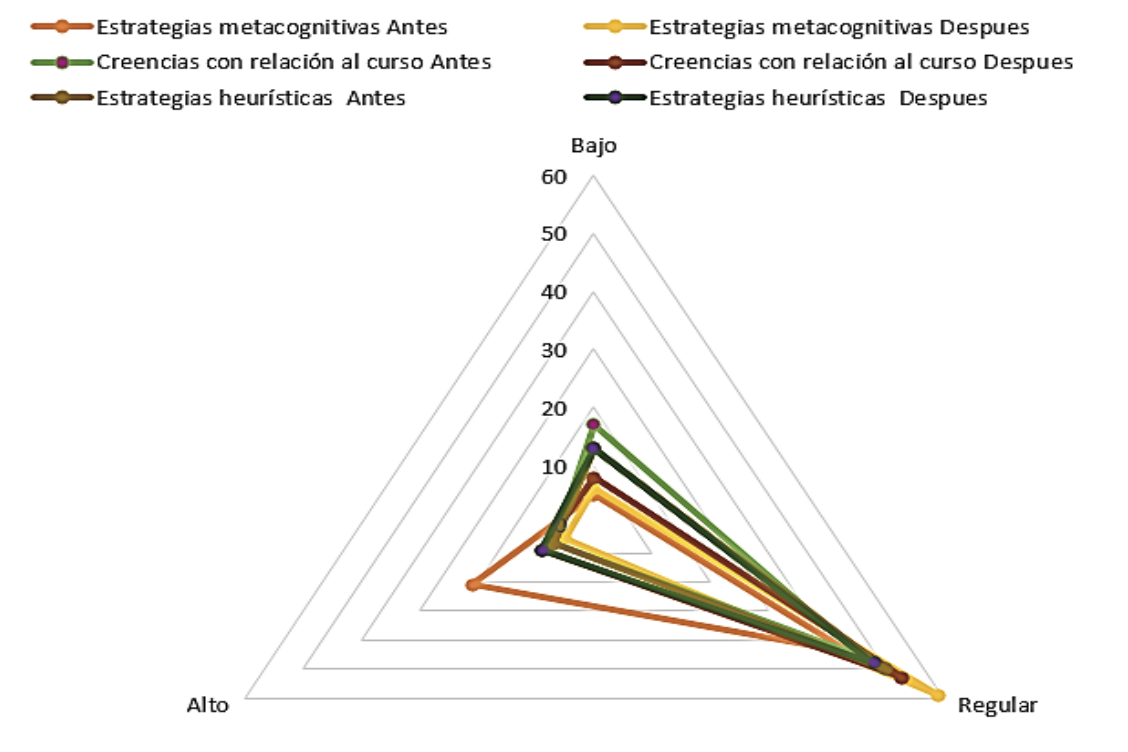
Figura 2. Resumen de la percepción de los estudiantes acerca de las Estrategias Metacognitivas, estrategias heurísticas y creencias con relación al curso
Los resultados obtenidos sugieren que en tres de las estrategias resolutivas que se aplicaron a los estudiantes se logró una leve mejora al ubicarse en los niveles medio y alto en virtud que hubo una disminución en el porcentaje de estudiantes ubicados en el nivel bajo antes de la intervención y un incremento en el nivel medio después de la intervención con la excepción de algún caso de disminución del porcentaje en el nivel alto, el cual se explicará posteriormente.
Además, en concordancia con los resultados descriptivos mostrados en los párrafos precedentes, se encontró significancia estadística en las Estrategias resolutivas de Allan Schoenfeld para la resolución de problemas matemáticos de alta demanda cognitiva referidas a los conocimientos previos y Creencias con relación al curso. En ese sentido, con el coeficiente de Pearson se obtuvo un p-valor (p-valor<0.01) menor al supuesto (p-valor<0.05) consiguiéndose una correlación positiva en todos los casos (ρPearson > 0.76).
4. Discusión de resultados
Con relación a los resultados obtenidos en la Prueba de conocimientos previos después de la intervención pedagógica, estos mostraron que hubo una mejora significativa en cuanto al porcentaje en el nivel En proceso y una leve mejora en el nivel Logrado. Esto quiere decir los estudiantes fueron capaces de incrementar sus conocimientos matemáticos conforme se fue desarrollando cada una de las sesiones de clase de manera tal que su estructura mental logró unificar lo que sabía con lo nuevo que adquirió durante la intervención pedagógica. Para lograr un mejor desempeño en cuanto a resolver problemas matemáticos es importante poseer conocimientos previos sobre lo que se está abordando en cada situación problemática dado que permite que los estudiantes exploren entre lo que ya saben y vean las conexiones con la tarea en cuestión (Coskun & Bostan, 2018; Norqvist 2018; Hong & Choi 2019; Radmehr & Drake, 2018) los cuales de preferencia deben estar contextualizados (Gijsbers et al., 2019).
Lo deseable es que todos los estudiantes hubiesen alcanzado el nivel Logrado para enfatizar una relación favorable entre ambas variables de estudio, sin embargo, el incremento en sus medias y niveles de logro a un nivel superior de donde se ubicaron inicialmente permite concluir que la hipótesis planteada se cumplió y podemos afirmar que si existe relación entre los conocimientos previos y la resolución de problemas matemáticos.
Respecto a las creencias en relación al curso, los resultados mostraron también que los estudiantes tuvieron una leve mejora en virtud que pasaron de estar en el nivel bajo a posicionarse en el nivel medio y algunos de los que se ubicaron en este nivel lograron ubicarse en el nivel alto. A partir de estos resultados podemos concluir que las creencias de los estudiantes de la población en estudio se encuentran ligadas a la concepción que tienen de la matemática y por ende, en el proceso de solución de problemas. Es sabido por todos que la matemática como curso en si presenta ciertas creencias que limitan al estudiante a tener un mejor desempeño, si a eso se le suma que nunca se le explicó la razón de su utilidad con situaciones concretas acorde a su contexto y solo se le presentó problemas de alta complejidad entonces sus creencias de una matemática difícil influirá cuando tenga que resolver problemas matemáticos.
Al contextualizar los problemas, Prendergast et al., (2018) sugiere que las creencias de los estudiantes sobre la utilidad del curso tienen relación con su desempeño en la resolución de problemas por lo que deja en claro que existe un vínculo entre las creencias de los estudiantes sobre la resolución de problemas en matemáticas y su desempeño en la materia. La gran mayoría de estudiantes manifiesta ciertas creencias según como haya sido su experiencia en años anteriores, según como lo han experimentado sus padres o incluso sus mismos docentes. Es conveniente detallar que muchos estudiantes consideran que el docente es quien tiene la verdad absoluta y seguir sus reglas es más que suficiente. De este modo, por ejemplo, aunque el docente nunca le haya dicho al estudiante que conocer matemáticas es memorizar y aplicar las reglas, como eso fue lo que en la práctica siempre hizo, eso es lo que le queda al estudiante en su cabeza. El conocimiento de los docentes sobre la materia y el contenido pedagógico influye en su interacción con sus estudiantes al participar en actividades matemáticas escolares y se ve reflejado en la forma en que estos piensan puesto que afectan las sugerencias e ideas de los estudiantes, por una parte, y los profesores, por otra, tienden a guiar a los estudiantes hacia su solución preferida (Raveh & Shaharabani, 2019). Los métodos de instrucción de los docentes en las actividades de resolución de problemas matemáticos también pueden influir en el disfrute, el valor, el interés y la autoeficacia de sus alumnos (Shahbari, 2017). Diversos estudios concluyen que modificar las creencias es un proceso paulatinamente lento que puede conllevar años. Aun así, en el corto tiempo que duró la intervención pedagógica se logró movilizar a buen porcentaje de estudiantes a un nivel de logro esperado.
Por otra parte, los resultados respecto a las estrategias heurísticas sugieren que los estudiantes mostraron un leve aumento en cuanto a sus conocimientos y utilización en relación a ellas dado al porcentaje en el nivel alto obtenido después de la intervención pedagógica (véase la figura 2) destacándose que estudiantes que estuvieron en este nivel inicialmente lograron ubicarse posteriormente en el nivel alto. Es preciso señalar que muchos de los estudiantes ubicados en el nivel medio continuaron en este mismo nivel después de la aplicación de las sesiones de clase demostrando que no hubo mejora alguna excepto mejora en sus puntajes que los seguía ubicando en el mismo nivel. Con estos resultados, se concluye que para medir una relación entre ambas variables de estudio es necesario que los estudiantes tengan conocimiento sobre al menos algunas estrategias heurísticas, sepan en qué consisten y cómo utilizarlas. Los estudiantes no estuvieron habituados a utilizar estrategias heurísticas ni siquiera tenían conocimiento de ellas, en su mayoría asumían como estrategias heurísticas los diversos procesos que habían aprendido en forma repetitiva, tenían una concepción errónea. Por ello, los resultaron obtenidos son de gran relevancia ante el contexto señalado ya que evidencia que la relación entre los la resolución de un problema y las estrategias que utilizan se debe dar en forma homogénea y va en consonancia con Guven, et al., (2016) quien afirma que en los procesos matemáticos, hay una serie de cuestiones que afectan el proceso de resolución de problemas entre ellos el del conocimiento de un tema matemático adquirido durante el proceso de aprendizaje, las estrategias heurísticas que los estudiantes usan para determinar la estrategia apropiada para resolver un problema y estrategias de control que auditan el proceso de resolución de problemas.
El espíritu de este estudio estuvo enfocado en contribuir en la reflexión y utilización de estrategias heurísticas por parte de los estudiantes en el momento que se enfrentan a la solución de un problema, pero no a cualquier problema sino a aquellos que tengan una alta demanda cognitiva guiados de forma planificada y consciente. Lo que se quiso es que los estudiantes se apropiaran de las estrategias utilizadas, que sepan cómo y cuándo emplearlas, de qué forma lo están haciendo; que es lo que saben y lo que no saben poniendo en práctica sus habilidades heurísticas y metacognitivas, sus creencias y sus conocimientos previos a la hora de resolver un problema. Es decir, lo que se busca es tal como lo afirman Klymchuk, (2017); Kitchen (2020); Norqvist (2017) y Hong & Choi (2019) ir más allá del mero hecho de hacer matemáticas mecánicamente solo por cumplir con las actividades escolares sin un verdadero aprendizaje.
Con respecto a las Estrategias Metacognitivas, los resultados obtenidos demostraron que la mayoría de estudiantes se ubicaron en el nivel medio con disminución de porcentaje de estudiantes en el nivel alto. Con estas estrategias ocurrió el mismo escenario que con las estrategias heurísticas, no se logró demostrar la hipótesis de relación entre ambas variable (solución de problemas y estrategias metacognitivas) ya que la mayoría de estudiantes continuó en el nivel medio antes y después de la intervención pedagógica. Ante estos resultados es preciso detallar que las características de la enseñanza de la matemática antes de la aplicación de las sesiones de clase en la población en estudio fue exclusivamente algorítmica (resolución de ejercicios del mismo tipo) y evaluar el proceso metacognitivo en sí mismo no era de gran relevancia ya que se repetían procedimientos resolutivos, en cambio, al aplicar las sesiones con situaciones problemáticas de alta demanda cognitiva cuyas conexiones matemáticas para resolverlas exigía análisis, razonamiento, interpretación, búsqueda de estrategias por parte de los estudiantes implicó evaluar los procesos metacognitivos que debían aplicar y que estos diferían de lo que inicialmente concebían. Esta es la razón por la que en el nivel alto haya un descenso en el porcentaje de estudiantes y la gran mayoría se ubicara en el nivel medio. Uno de los aportes de este estudio es precisamente el abordaje del fenómeno de los estudiantes comprobando sus soluciones a través de la lente de la metacognición y resolución de problemas dados que la mayor parte de los estudios se han realizado en el contexto de las matemáticas escolares.
La mayoría de los autores consultados coinciden que para lograr resolver problemas matemáticos es importante que el estudiante sepa monitorear y regular su proceso de manera que pueda decidir cuándo abandonar un camino exitoso y tomar uno nuevo. En otras palabras, mirar en retrospectiva la solución dada a un problema matemático y reflexionar críticamente acerca de la validez del razonamiento empleado y si hay más de una vía en la que pueda solucionarse de manera creativa (Kontorovich, 2019). Por otra parte, puede argüirse que cuanto mayor sea la capacidad en relación a Estrategias Metacognitivas que posean los estudiantes, mayor será el nivel de logro alcanzado en su capacidad para resolver problemas matemáticos de contexto.
Finalmente, es importante precisar que se tomó como referencia la prueba Pisa en la selección de los reactivos para la construcción de la prueba de contexto dado que por ser una prueba internacional debidamente validada, ofrece un abanico de posibilidades para el diseño de problemas matemáticos de alta demanda cognitiva que permite entrelazar las relaciones y procedimientos que requieren conocer y aplicar conocimientos, estrategias, procedimientos exigiendo al mismo tiempo la autorregulación en la búsqueda del camino de solución utilizado. Es decir, dicha prueba resume la experiencia acumulada a lo largo del tiempo en diferentes países respecto de las competencias matemáticas mínimas que deben alcanzar los estudiantes y socializar la experiencia con todos los interesados en la enseñanza y aprendizaje de las matemáticas en la educación secundaria. Además, sugiere reflexionar acerca de la praxis docente en lo que respecta a contenidos y estrategias didácticas en la administración de un curso acerca de su comprensión de las matemáticas elementales, obtener conocimientos sobre la instrucción basada en la indagación al experimentar ellos mismos dicha pedagogía y aprendan de primera mano sobre el valor potencial de ser miembros de una comunidad en la que todos se realimentan de todos (Kitchen 2020).
5. Conclusiones
A partir del análisis del tratamiento estadístico y de la discusión de resultados se concluye para este trabajo de investigación que no todas las estrategias resolutivas propuestas por Allan Schoenfeld se relacionan con la solución de problemas matemáticos de alta demanda cognitiva. Es preciso destacar que los conocimientos previos y las creencias en relación al curso fueron las estrategias que presentaron una mejor relación con la variable dependiente. Hubo factores que pudieron haber influido en los estudiantes respecto al desarrollo de las otras dos estrategias resolutivas que condicionaron los resultados. A pesar de ello, los resultados en las calificaciones en la prueba de contexto después de la intervención pedagógica ubicaron a la mayoría de estudiantes en los niveles En proceso y Logrado, ambos niveles considerados como esperados (favorables de acuerdo a las características de nuestro sistema educativo).
La importancia de esta investigación tal como lo establece Coskun & Bostan (2018) es que la selección de las tareas dadas que son una parte integral del pensamiento matemático, del aprendizaje y de la enseñanza, sobre todo en lo que respecta a la conceptualización, la generalización, la abstracción, la argumentación y el pensamiento analógico su selección debe hacerse tomando como base el perfil de los estudiantes, los objetivos de los programas y las estrategias didácticas que mejor conjuguen ambos elementos. (Olivares, & Segovia, 2020).
Asimismo para Hong & Choi (2019), los factores que pueden ayudar a mantener la demanda cognitiva son la utilización de los conocimientos previos del alumno, el andamiaje, el tiempo de espera adecuado, la presión sostenida para las explicaciones y el autocontrol del estudiante sobre la base de la utilidad de lo que está aprendiendo. Por otro lado, los factores que pueden disminuir la demanda cognitiva son la inadecuación de las tareas, el exceso o la falta de tiempo, el cambio de enfoque hacia la respuesta correcta y que los docentes se hagan cargo de las discusiones en clase. De allí que la planificación previa de las tareas es de suma importancia en virtud que esta incide en el desempeño de los estudiantes al resolver problemas matemáticos (Monarrez & Tchoshanov 2020).
La intervención pedagógica basada en el desarrollo de estrategias resolutivas propuestas por Allan Schoenfeld demostró cierto nivel de eficacia en cuanto a la resolución de problemas matemáticos. En ese sentido, el aislamiento de los determinantes clave de la dificultad de los problemas; la identificación de las características de los buenos solucionadores de problemas; el entrenamiento en heurística, metacognición, factores afectivos y creencias; y el análisis de la interacción social, el planteamiento de problemas, la evaluación, las representaciones y el uso de la tecnología para resolver problemas son aspectos a considerarse en la planificación pedagógica en el aula (Olivares, & Segovia, 2020). Futuras líneas de investigación podrían estar orientadas hacia el estudio del componente matemático expresado en competencias del currículo de educación básica y su correspondencia con cada uno de los niveles de desempeño matemático buscado a través de la prueba PISA de tal forma que la praxis docente en palabras de Tsai & Li, (2017) trascienda el medir solo el rendimiento de los estudiantes en el sentido de las puntuaciones obtenidas y se logre fomentar el desarrollo educativo de ellos en su capacidad para resolver problemas matemáticos de alta demanda cognitiva.
6. REFERENCIAS BIBLIOGRÁFICAS
Campbell, T., Boyle, J., & King, S. (2020). Proof and argumentation in K-12 mathematics: a review of conceptions, content, and support. International Journal of Mathematical Education in Science and Technology, 51(5), 754-774. https://doi.org/10.1080/0020739X.2019.1626503
Coskun, S., & Bostan, M. (2019). An in-service primary teacher’s implementation of mathematical tasks: the case of length measurement and perimeter instruction. International Journal of Mathematical Education in Science and Technology, 50(4), 486-505. https://doi.org/10.1080/0020739X.2018.1522675
Gijsbers, D., Putter-Smits, L., & Pepin, B. (2020) Changing students’ beliefs about the relevance of mathematics in an advanced secondary mathematics class. International Journal of Mathematical Education in Science and Technology, 51(1), 87-102. https://doi.org/10.1080/0020739X.2019.1682698
Guven, B., Aydin-Guc, F., & Ozmen, Z. (2016). Problem types used in math lessons: the relationship between student achievement and teacher preferences. International Journal of Mathematical Education in Science and Technology, 47(6), 863-876. https://doi.org/10.1080/0020739X.2015.1136438
Hammad, S., Graham, T., Dimitriadis, C., & Taylor, A. (2020). Effects of a successful mathematics classroom framework on students’ mathematics self-efficacy, motivation, and achievement: a case study with freshmen students at a university foundation programme in Kuwait. International Journal of Mathematical Education in Science and Technology, 53(6), 1502-1527. https://doi.org/10.1080/0020739X.2020.1831091
Hong, D., & Choi, K. (2019). Challenges of maintaining cognitive demand during the limit lessons: understanding one mathematician’s class practices. International Journal of Mathematical Education in Science and Technology, 50(6), 856-882. https://doi.org/10.1080/0020739X.2018.1543811
Jäder, J., Lithner., J., & Sidenvall, J. (2019) Mathematical problem solving in textbooks from twelve countries. International Journal of Mathematical Education in Science and Technology, 51(7), 1120-1136. https://doi.org/10.1080/0020739X.2019.1656826
Kitchen, R. (2020). The power of their ideas: leveraging teachers’ mathematical ideas in professional development. International Journal of Mathematical Education in Science and Technology, 1-25. https://doi.org/10.1080/0020739X.2020.1847337
Klymchuk, S. (2017). Puzzle-based learning in engineering mathematics: students’ attitudes. International Journal of Mathematical Education in Science and Technology, 48(7), 1106-1119. https://doi.org/10.1080/0020739X.2017.1327088
Kontorovich, I. (2019). Non-examples of problem answers in mathematics with particular reference to linear algebra. The Journal of Mathematical Behavior, (54), 100674-100685. https://doi.org/10.1016/j.jmathb.2019.01.001
Lane, C., Stynes, M., & O'Donoghue, J. (2016) Post-primary students’ images of mathematics: findings from a survey of Irish ordinary level mathematics students. International Journal of Mathematical Education in Science and Technology, 47(7), 1009-1027. https://doi.org/10.1080/0020739X.2016.1170899
Monarrez, A., & Tchoshanov, M. (2020). Unpacking teacher challenges in understanding and implementing cognitively demanding tasks in secondary school mathematics classrooms. International Journal of Mathematical Education in Science and Technology, 1-20. https://doi.org/10.1080/0020739X.2020.1857860
Norqvist, M. (2018). The effect of explanations on mathematical reasoning tasks. International Journal of Mathematical Education in Science and Technology, 49(1), 15-30. https://doi.org/10.1080/0020739X.2017.1340679
Olivares, D., Lupiáñez, J., & Segovia, I. (2020). Roles and characteristics of problem solving in the mathematics curriculum: a review. International Journal of Mathematical Education in Science and Technology, 52(7), 1079-1096, https://doi.org/10.1080/0020739X.2020.1738579
PISA (2012). Primeros Resultados. Informe Nacional del Perú. Ministerio de Educación.
Prendergast, M., Breen, C., Bray, A., Faulkner, F., Carroll, B., Dominic, Q., & Michael, C. (2018). Investigating secondary students beliefs about mathematical problem-solving. International Journal of Mathematical Education in Science and Technology, 49(8), 1203-1218. https://doi.org/10.1080/0020739X.2018.1440325
Radmehr, F & Drake, M. (2019). Revised Bloom’s taxonomy and major theories and frameworks that influence the teaching, learning, and assessment of mathematics: a comparison. International Journal of Mathematical Education in Science and Technology, 50(6), 895-920. https://doi.org/10.1080/0020739X.2018.1549336
Raveh, I., & Shaharabani, Y. (2019). Experienced engineers becoming mathematics teachers: preliminary perceptions of mathematics teaching. International Journal of Mathematical Education in Science and Technology, 50(8), 1223-1240. https://doi.org/10.1080/0020739X.2019.1626501
Schoen, R., LaVenia, M., & Ozsoy, G. (2019). Teacher beliefs about mathematics teaching and learning: Identifying and clarifying three constructs. Cogent Education, 6(1), https://doi.org/10.1080/2331186X.2019.1599488
Shahbari, J. (2017). Mathematics teachers’ conceptions about modelling activities and its reflection on their beliefs about mathematics. International Journal of Mathematical Education in Science and Technology, 49(5), 721-742. https://doi.org/10.1080/0020739X.2017.1404650
Tisdell, C. (2020). Tic-Tac-Toe and repeated integration by parts: alternative pedagogical perspectives to Lima's integral challenge. International Journal of Mathematical Education in Science and Technology, 51(3), 424-430. https://doi.org/10.1080/0020739X.2019.1620969
Tsai, T., & Li, H. (2017). International comparative studies in mathematics education: are we obsessed with the international rankings of measured educational outcomes? International Journal of Mathematical Education in Science and Technology, 48(8), 1262-1267. https://doi.org/10.1080/0020739X.2017.1315189